Compositions de familles de fonctions

[Dinozzo13]

Bonjour, j'ai inventé un exercice et j'aimerais avoir votre avis, merci ^^.
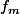
On se donne une famille de fonction définies par , .
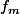
Je cherche à déterminer la fonction composée avec elle-même n fois, , c'est-à-dire : .
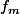
Sachant que pour , , car est composée avec elle-même 1 fois.

Voilà ce que j'aurai dit :
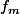
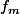
est définie sur donc est définie sur . Par conséquent, à chaque fois que l'on composera avec elle-même, la fonction composée sera toujours définie sur .



Après d'autres calculs de fonctions composée successives, je trouve :
.
Et après il suffit de vérifier par récurrence.
Est-ce que mon raisonnement paraît correct ? :ptdr:

[girdav]

Bonjour.
Le raisonnement est correct.
On peut écrire plus simplement, en définissant puis en écrivant

Tu peux généraliser avec

[lapras]

salut,
je trouves que tu te compliques la vie.
En effet, définie
U_n = f_m itérée n fois
U_{n+1} = f_m(U_n)=-mU_n + 1
ca fait une suite arithméco géométrique, tu peux faire un changement de variable et te rammener à une suite géométrique, et c'est fini. :)

[Dinozzo13]

Bonjour.
Le raisonnement est correct.
On peut écrire plus simplement, en définissant puis en écrivant

Tu peux généraliser avec

pourquoi tu met le n avec le m dans ? il n'y a qu'un paramètre.

salut,
je trouves que tu te compliques la vie.
En effet, définie
U_n = f_m itérée n fois
U_{n+1} = f_m(U_n)=-mU_n + 1
ca fait une suite arithméco géométrique, tu peux faire un changement de variable et te rammener à une suite géométrique, et c'est fini.

J'ai voulu le faire sans les suites arithméco-géométriques

[Dinozzo13]

Bonjour.
Tu peux généraliser avec

J'ai essayer et je trouve :
.
Avec n : le nombre de fois que la fonction est composée avec elle-même ().
Bien sur toutes les fonctions composées sont définies sur

[girdav]

pourquoi tu met le n avec le m dans f_{m,n} ? il n'y a qu'un paramètre.

Oui mais indique le nombre de compositions.