bonjour,pourriez vous m'aider?
M'=f(M)
Z=(z-4+3i)/(iz+1)
1)calculer(2i+1) au carré.en déduire les points invariants de f
2)a)soit x+iy la forme algébrique de z,déterminer en fonction de x et y la forme algébrique de Z
b)déterminer et représenter l'ensemble des points M d'affixes z tels que Z soit réel,puis Z soit imaginaire pur
merci
Complexes term s
8 messages
- Page 1 sur 1
par Frangine » 27 Jan 2006, 14:15
bonjour,
Tu as commencé quelquechose ?
Si tu ne sais pas par où commencer, je te donne un conseil : apprendre son cours en reisant ses notes ou son bouquin..
C'est une application directe du cours.
Tu as dû faire au moins 1 exo de ce genre en classe.
Bon travail
Tu as commencé quelquechose ?
Si tu ne sais pas par où commencer, je te donne un conseil : apprendre son cours en reisant ses notes ou son bouquin..
C'est une application directe du cours.
Tu as dû faire au moins 1 exo de ce genre en classe.
Bon travail
par allomomo » 27 Jan 2006, 19:36
Salut,
données :
 \rightarrow M'(z'))
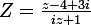
1 -^2=(2i)^2+4i+1=-3+4i)
2 - On pose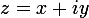
-4+3i}{i(x+iy)+1}=\frac{(x-4)+i(y+3)}{(1-y)+ix}=\frac{[(x-4)+i(y+3)]}{[(1-y)+ix]} \times \frac{[(1-y)-ix]}{[(1-y)-ix]})
(1-y)+x(y+3)}{(1-y)^2+x^2}+i\frac{(y+3)(1-y)-x(x-4)}{(1-y)^2+x^2}= \frac{4x+4y-4}{(1-y)^2+x^2}-i\frac{x^2-4x+y^2-2y-3}{(1-y)^2+x^2})
3 -=0)
et 
différent de i !
donc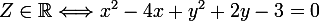
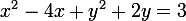
^2-(\frac{4}{2})^2+(y+\frac{2}{2})^2-(\frac{2}{2})^2=3)
^2+(y+1)^2=3+(\frac{4}{2})^2+(\frac{2}{2})^2=8)
Soit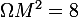
donc 
E (=L'ensemble des points M d'affixes z tels que Z soit réel) est le cercle de centre)
et de rayon 
privé du point )
4 -=0)
et différent de i !
donc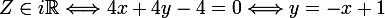
F (=L'ensemble des points M d'affixes z tels que Z soit imaginaire pur) est la droite d'équation
privé du point
voila
données :
1 -
2 - On pose
3 -
donc
Soit
E (=L'ensemble des points M d'affixes z tels que Z soit réel) est le cercle de centre
4 -
donc
F (=L'ensemble des points M d'affixes z tels que Z soit imaginaire pur) est la droite d'équation
voila
par Mikou » 27 Jan 2006, 19:51
par allomomo » 27 Jan 2006, 20:15
si tu ne comprends pas quelque chose tu demandes, je pense que c'est très clair
par Mikou » 28 Jan 2006, 09:13
ok allomomo, merci pour la reponse par pm. Au final ma solution et la tienne donnent le meme resultat sauf que tu te trompes le centre c'est 
:happy3:
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :