Complexes....
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Nov 2006, 13:19
par sue » 12 Nov 2006, 13:19
bonjour,
j'ai un autre exo sur les complexes ..
soit
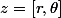
t.q

on considère : Z = |z|+z
-Déterminer le module et l'argument de z
- déterminer l'ensemble de points M(z) lorsque M'(Z) varie sur le cercle C de centre O(0,0)
-----
1)je trouve que
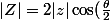)
et
 = \frac{\theta}{2})
.
2) il me semble que c'est le cercle de centre O et de rayon
}{2})
en posant r' le rayon de C , mais bon ce n'est que de l'intuition :triste:
pourriez-vous m'aiguiller ?
MERCI
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 12 Nov 2006, 13:48
par Quidam » 12 Nov 2006, 13:48
sue a écrit: 1)je trouve que
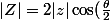)
et
 = \frac{\theta}{2})
.
Je suis d'accord !
sue a écrit: 2) il me semble que c'est le cercle de centre O et de rayon
}{2})
en posant r' le rayon de C , mais bon ce n'est que de l'intuition :triste:
Pas d'accord ! C'est quoi
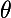
dans ta formule ? Il n'y a pas de
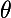 donné
donné dans l'énoncé !
J'ai commencé, mais je n'ai guère le temps ! Il semble que l'équation de la courbe en question soit un peu compliquée...Mais il me faut plus de temps ! Ca se simplifie peut-être au dernier moment ...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Nov 2006, 14:04
par sue » 12 Nov 2006, 14:04
ben

c'est l'angle tetha , l'argument de z .
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 12 Nov 2006, 14:35
par Quidam » 12 Nov 2006, 14:35
sue a écrit: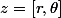
t.q

on considère : Z = |z|+z
- déterminer l'ensemble de points M(z) lorsque M'(Z) varie sur le cercle C de centre O(0,0)
sue a écrit:ben

c'est l'angle tetha , l'argument de z .
Quidam a écrit:C'est quoi
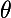
dans ta formule ? Il n'y a pas de
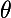 donné
donné dans l'énoncé !
On te demande : déterminer l'ensemble de points M(z) lorsque M'(Z) varie sur le cercle C de centre O(0,0)
et tu réponds :
2) il me semble que c'est le cercle de centre O et de rayon }{2}) en posant r' le rayon de C
en posant r' le rayon de CIl n'y a pas de
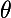
dans l'énoncé ? De quel
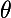
parles-tu ? Comment veux-tu tracer ton cercle de rayon
}{2})
sans connaître la valeur de
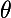
? Essaie donc de le tracer ton cercle ! Tu ne peux pas, si tu ne connais pas
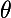
!
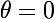
?
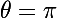
,
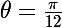
?????
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Nov 2006, 14:39
par sue » 12 Nov 2006, 14:39
ok , j'ai compris ce que tu voulais dire ..
sinon qu'est-ce que dois faire mnt ? une piste ?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 12 Nov 2006, 19:18
par Quidam » 12 Nov 2006, 19:18
De
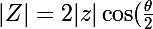)
, et de
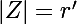
on obtient immédiatement :
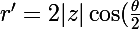)
Soit :
})
ce qui indique que les points en question appartiennent à la courbe d'équation polaire :
})
L'équations cartésienne correspondante est du quatrième degré (il me semble) et pas vraiment du niveau Terminale S ! Pas plus que l'équation polaire d'ailleurs.
J'imagine que le professeur attends simplement que tu donnes cette équation comme réponse :
})
Pour info, je l'ai tracée ci-dessous pour que tu voies à quoi cela ressemble :

Je suis tellement étonné du résultat que je me demande bien si je n'ai pas fait une erreur grossière !
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Nov 2006, 19:36
par sue » 12 Nov 2006, 19:36
merci Quidam ...
pour la représentation graphique , c'est celle qui ressemble à une partie d'une ellipse ?
et pour l'équation polaire comment puis-je la transformer en équation cartésienne ?
merci encore !
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Nov 2006, 20:01
par sue » 12 Nov 2006, 20:01
c'est pas par hasard l'équation polaire d'une parabole :hein:
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 12 Nov 2006, 20:35
par Quidam » 12 Nov 2006, 20:35
sue a écrit: pour la représentation graphique , c'est celle qui ressemble à une partie d'une ellipse ?
Je joins une autre image à plus petite échelle pour que tu voies que ça ne ressemble vraiment pas à une ellipse (il y a des points à l'infini !)
Les points de cette courbe sont transformés en des points du demi-cercle de droite, comme tu peux le constater sur quelques points...
Pour obtenir l'équation cartésienne, tu peux écrire :
}{2\cos(\frac{\theta}{2})}= r' \sin(\frac{\theta}{2}))
, d'où tu extrait
)
fonction de y.
Par ailleurs, tu as
)
fonction de r et r'.
Et ensuite tu élimine

...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Nov 2006, 20:51
par sue » 12 Nov 2006, 20:51
re,
tu veux dire que je dois faire comme ça :
on a
 = \frac{y}{r'})
et
 = \frac{r'}{2r})
donc

est-ce ça ?
mais dites moi d'abord , pourquoi on écrit
}{2\cos(\frac{\theta}{2})}= ...)
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Nov 2006, 00:48
par Quidam » 13 Nov 2006, 00:48
sue a écrit:re,
tu veux dire que je dois faire comme ça :
on a
 = \frac{y}{r'})
et
 = \frac{r'}{2r})
donc

est-ce ça ?
mais dites moi d'abord , pourquoi on écrit
}{2\cos(\frac{\theta}{2})}= ...)
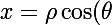)
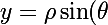)
Si
})
alors
} \sin(\theta))
}{2\cos(\frac{\theta}{2})})
-
crassus
- Membre Relatif
- Messages: 208
- Enregistré le: 06 Nov 2006, 22:21
-
 par crassus » 13 Nov 2006, 01:03
par crassus » 13 Nov 2006, 01:03
je me demande si tu n'as pas intervertis M et M' dans la deuxième question ...
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Nov 2006, 01:10
par Quidam » 13 Nov 2006, 01:10
crassus a écrit:je me demande si tu n'as pas intervertis M et M' dans la deuxième question ...
Bonne question ! J'espère bien que non !
-
crassus
- Membre Relatif
- Messages: 208
- Enregistré le: 06 Nov 2006, 22:21
-
 par crassus » 13 Nov 2006, 01:14
par crassus » 13 Nov 2006, 01:14
il s'agirait de translater un cercle ... ce qui me parait plus en accord avec le niveau ...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 13 Nov 2006, 02:17
par sue » 13 Nov 2006, 02:17
crassus a écrit:je me demande si tu n'as pas intervertis M et M' dans la deuxième question ...
je me demandais bien la même chose mais il s'agit bel et bien de ''...lorsque M'(Z) varie sur le cercle de centre O(0,0) ''
mais c'est vrai que parfois notre prof nous met des petits casse-têtes pour introduire une nouvelle leçon :hum: ya-t-il un rapport avec les coniques ? normalement c'est la leçon suivante ...
merci beaucoup pour votre aide :we:
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Nov 2006, 10:35
par Quidam » 13 Nov 2006, 10:35
sue a écrit:c'est vrai que parfois notre prof nous met des petits casse-têtes pour introduire une nouvelle leçon :hum: ya-t-il un rapport avec les coniques ? normalement c'est la leçon suivante ...
Oui, petit galopin ton prof !
En tous cas il est clair que ce n'est pas une conique. La courbe, c'est facile de le constater, est entièrement contenue entre les deux droites d'équations respectives y=r' et y=-r'. La seule conique compatible avec cette limitation est l'ellipse, et l'on a vu que ce n'est pas une ellipse, puisqu'elle a deux branches infinies...
Un feed-back serait apprécié après que le professeur aura donné la correction de son devoir...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 14 Nov 2006, 10:23
par sue » 14 Nov 2006, 10:23
bonjour,
je reviens sur ce problème.. :mur:
supposons qu'il s'agit bien de l'ensemble de point M'(Z) lorsque M(z) varie sur le cercle C de centre O(0,0) .
comment puis-je démontrer qu'il s'agit de translater le cercle C comme l'avait déjà signalé Crassus ?
merci encore et encore :we:
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 14 Nov 2006, 11:42
par Quidam » 14 Nov 2006, 11:42
Ben ça, au contraire, c'est super évident ! Si M(z) varie sur un cercle de centre O et de rayon r, cela implique que |z|=r ! Donc la formule devient, dans ce cas particulier : Z = z+r.
Il s'agit bien de la translation de vecteur

, non ?
-
maturin
- Membre Irrationnel
- Messages: 1193
- Enregistré le: 09 Nov 2006, 16:28
-
 par maturin » 14 Nov 2006, 11:50
par maturin » 14 Nov 2006, 11:50
pour passer de polaire à cartésien et inversement tu utilises:
y=rho.sin(theta)
x=rho.cos(theta)
excusez, j'ai un train de retard... pas vu la 2eme page...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 14 Nov 2006, 11:57
par sue » 14 Nov 2006, 11:57
Ben ça, au contraire, c'est super évident ! Si M(z) varie sur un cercle de centre O et de rayon r, cela implique que |z|=r ! Donc la formule devient, dans ce cas particulier : Z = z+r.
Il s'agit bien de la translation de vecteur , non ?
oui ok , mais quand j'ai essayé d'écrire l'équation polaire de l'ensemble de points M'(Z) , ça me donne pas l'équation d'un cercle :hein:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités

