Complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2018, 10:36
par Majaspique » 20 Jan 2018, 10:36
Bonjour,
voici l'exercice :
On considère le point A d'affixe 2 et le point B d'affixe -2. A tout point M différent de A, et d'affixe z, on associe le point M' d'affixe z' donné par z' =
-2})
.
1: a: Démontrer que |z'| = 2
|z'| = -2}|)
|z'| = -4}{x-iy-2}|)
|z'| = }{(x-iy-2)}|)
|z'| = 
|z'| = ^2+(0)^2})
|z'| = 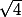
|z'| =  Est-ce juste ?
Est-ce juste ?b: En déduire une indication sur la position du point M'.
On peut en déduire que comme |z'| = |z(A)|, les points A et M' sont confondus.Est-ce juste ?2 : Déterminer l'ensemble E des points M d'affixe z (z

2) tels que M' = B.
Là je bloque puisqu'on ne peut pas faire |z'| = -2.Pourriez-vous m'aider s'il vous plaît ?
-
aviateur
 par aviateur » 20 Jan 2018, 11:35
par aviateur » 20 Jan 2018, 11:35
Bonjour
Pour le 1. on ne peut pas dire que c'est faux mais le passage de la 3ème égalité tu l'expliques comment?
Ensuite |2|=2 (tout le monde le sait) alors pourquoi passer par Rome pour aller de la Gare du Nord à la Gare Montparnasse?
Maintenant |z'|=2 : sait tu ce que c'est un module? Est ce que tu vois les complexes géométriquement?
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2018, 12:45
par Majaspique » 20 Jan 2018, 12:45
Le passage à la 3ème égalité s'explique par :
|z'| =

|z'| = 2 veut dire que la distance OM' = 2 ?
-
aviateur
 par aviateur » 20 Jan 2018, 14:12
par aviateur » 20 Jan 2018, 14:12
Non c'est la ligne d'après que je demande. Elle est bonne mais vu l'ensemble j'ai un gros doute sur ta compréhension. Tu est en quelle classe?
Maintenant OM'=2 cela veut dire que la distance de O à M' vaut 2. Cela veut dire quoi quant à la position du point M'
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2018, 15:08
par Majaspique » 20 Jan 2018, 15:08
Je suis en Terminale S.
Pour le passage à la 3ème égalité je n'ai juste pas vu qu'il y avait un + en haut et un - en bas j'ai donc considéré les deux expressions comme parfaitement identique et j'ai simplifié. Mais puisque les deux expressions sont différentes, y'a-t-il un moyen de simplifier cela autrement ?
Cela veut dire que M' est quelque part sur le cercle C(O;2) ?
-
aviateur
 par aviateur » 20 Jan 2018, 15:15
par aviateur » 20 Jan 2018, 15:15
Je ne m'occupe pas du facteur 2 pour l'instant
tu as un rapport (x-2+i y)(x-2-i y) ; tu dois voir que les deux nombres sont conjugués donc ils ont le même module
et comme le module d'un quotient c'est le quotient des modules, il vient que ce rapport est de module 1.
Multiplié par 2 tu as le résultat.
Pour le cercle c'est cela.
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2018, 15:29
par Majaspique » 20 Jan 2018, 15:29
donc si je fais :
|z'| =
}{(x-2-iy)}|)
|z'| =

|z'| =

la simplification est justifiée ?
Et pour la question 2, pourriez-vous m'aiguiller ?
Modifié en dernier par
Majaspique le 20 Jan 2018, 15:46, modifié 1 fois.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 20 Jan 2018, 15:36
par Pisigma » 20 Jan 2018, 15:36
Bonjour,
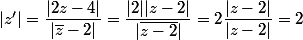
-
aviateur
 par aviateur » 20 Jan 2018, 15:48
par aviateur » 20 Jan 2018, 15:48
Non elle n'est pas justifiée à ton niveau. La justification je l'ai faite littéralement mais dans la pratique
on l'écrit symboliquement, c'est exactement ce que Pisigma a écrit.
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2018, 15:55
par Majaspique » 20 Jan 2018, 15:55
Mais |z(barre)-2|= conjugué de |z(barre)-2| = |z + 2| non ?
donc |z'| =

Quant-à la question 2, pourriez-vous m'aiguiller ?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 20 Jan 2018, 16:05
par Pisigma » 20 Jan 2018, 16:05
ton "égalité " de module est fausse; tu peux vérifier en calculant le module dans les 2 membres de ta relation
-
aviateur
 par aviateur » 20 Jan 2018, 16:06
par aviateur » 20 Jan 2018, 16:06
en latex conjugué cela s'écrit \bar{z}
Maintenant d'où sors-tu tes égalités , la première je veux bien, mais la deuxième???
La question 2. tu l'as mets en équation :
z'=-2 puis remplacer z' en fonction de z et résoudre l'équation.
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2018, 16:15
par Majaspique » 20 Jan 2018, 16:15
ça serait alors

=

= |z - 2| ?
Mais est-ce que

=

?
Pour la question 2 ce serait :
L'ensemble E des points M d'affixe z (z

2) tels que M' = B c'est à dire, tel que z' = -2 est le cercle C'(O;2) ? Ou ce serait OM' = OB donc la médiatrice à [M'B] privée de 2?
-
aviateur
 par aviateur » 20 Jan 2018, 20:04
par aviateur » 20 Jan 2018, 20:04
Pour tes 2 lignes c'est vrai.
Pour ta réponse à la question 2 il me semble l'avoir fait tout à l'heure mais j'ai oublié.
De mémoire l'ensemble des solutions est une droite.
Mais je ne comprends pas bien tes conclusions. Est ce que vraiment tu raisonnes avec logique?
Ici ce n'est pas la conclusion qui est important pour toi, c'est les étapes pour y arriver.
Je pense qu'il faut que tu fonctionnes pas à pas.
D'abord essayes de résoudre l'équation z'=-2 (en ayant remplacer z' en fonction de z). On ne sait pas ici, si tu l'as bien fait. N'ayant qu'une espèce de conclusion on ne peut rien dire si on ne sait pas comment tu as résolu ton équation.
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2018, 21:52
par Majaspique » 20 Jan 2018, 21:52
-
aviateur
 par aviateur » 20 Jan 2018, 23:28
par aviateur » 20 Jan 2018, 23:28
Non tu as fait une erreur les nombres 4 se s'éliminent pas.
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 21 Jan 2018, 00:13
par Majaspique » 21 Jan 2018, 00:13
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 21 Jan 2018, 07:39
par pascal16 » 21 Jan 2018, 07:39
2x=4, c'est pas x=4
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 21 Jan 2018, 07:48
par Majaspique » 21 Jan 2018, 07:48
Ah oui j'avais gardé la simplification du 0. Mais pour l'ensemble c'est juste si je modifie le x-4 par x-2 ?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 21 Jan 2018, 09:34
par pascal16 » 21 Jan 2018, 09:34
oui, on peut l'écrire aussi Re(z)=2, sachant que z ≠ 2.
Questions 1 et 2 :
(on) a calculé que pour un point du plan complexe, différent de A, son image était dans le cercle de centre 0 et de rayon 2. C'est une inclusion, c'est peut-être pas le cercle tout entier.
Question 3) :
On recherche l'antécédents d'un point, une condition nécessaire, c'est que sa norme soit de 2, car sinon, on sait qu'il n'a pas d'antécédent.
On cherche les antécédents s'ils existent de -2, qui est bien de norme 2, ses antécédents vont être une partie du plan (un ensemble de solutions).
Modifié en dernier par
pascal16 le 21 Jan 2018, 09:41, modifié 1 fois.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
