Bonsoir,
On a f une application..
f(x)= (i Z^2)/(Z+1)
Trouver sous forme trigonometrique puis sous forme algebrique les racines cubiques du nombre -1.
Doi-je faire l'application de [r,O]^3 = (i Z^2)/(Z+1) ou ya til une autre methode?(tel O=teta)
MERci pour tout
a bientot
Complexes.
7 messages
- Page 1 sur 1
Je n'ai pas mis -1=cos theta, mais cos pi = -1
Pour résoudre on suit la méthode suivante :
On note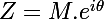 puisque un nombre complexe est noté avec son module et son argument. On utilise la notation exponentielle car elle est plus pratique pour les puissances.
puisque un nombre complexe est noté avec son module et son argument. On utilise la notation exponentielle car elle est plus pratique pour les puissances.
Z est une racine cubique de -1 ssi Z^3 = -1
Donc il ne reste plus qu'à résoudre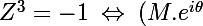^3 =-1 \; \Leftrightarrow \; M^3.e^{3i\theta} = -1)
-1 est situé sur l'axe des réels, à gauche. Son module est 1 donc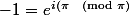})
On doit donc résoudre :
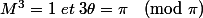
donc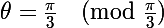
Les solutions sont donc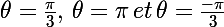
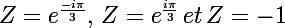
Pour résoudre on suit la méthode suivante :
On note
Z est une racine cubique de -1 ssi Z^3 = -1
Donc il ne reste plus qu'à résoudre
-1 est situé sur l'axe des réels, à gauche. Son module est 1 donc
On doit donc résoudre :
donc
Les solutions sont donc
re
:cry: :cry: On n'a pas vu en cours comment resoudre grace aux nombres complexes.
La seule methode était celle de mon premier post.
La seule methode était celle de mon premier post.
re
"l'application de [r,O]^3 = (i Z^2)/(Z+1"
Par example en cours, on a fait.
[r,O]^3 = [2, pi]
[r^3 ,3 O] = [2, pi]
r= 2^1/3
3 O=pi+2kpi
et on trouve ainsi les solutions voulues,juste dans le cas precedent ,ce n'étais pas assez simple comme ce cas,
Par example en cours, on a fait.
[r,O]^3 = [2, pi]
[r^3 ,3 O] = [2, pi]
r= 2^1/3
3 O=pi+2kpi
et on trouve ainsi les solutions voulues,juste dans le cas precedent ,ce n'étais pas assez simple comme ce cas,
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
