Complexes (niveau terminale S)

[Anonyme]

bonjour à tous!
j'ai un DM à faire pour la rentrée, et je n'arrive pas à faire cet exercice... j'aurai donc besoin de votre aide.

Le plan complexe P est rapporté à un repère orthonormal direct (O;u;v).
On désigne par A et B les points d'affixes respectives 1 et 4.
L'application f associe à tout point M d'affixe z de P, distinct de A, le point M' d'affixe Z définie par : Z=(z-4)/(z-1)

1) Soit C le point d'affixe i*racine de 2. déterminer l'affixe C'=f(C)

2) Démontrer que f admet 2 points invariants I et J. (on notera I celui d'ordonnée positive). (on rappelle qu'un point M est dit "invariant" par f lorsque f(M)=M).

3) Donner une interprétation géométrique de |Z|, |z-4|, |z-1|
En déduire l'ensemble D des points M d'affixe z tels que |Z|=1
Que peut-on dire de l'ensemble des images des points M de D ?

4) On pose z=x+iy et Z=X+iY avec x, y, X, Y réels.
a)déterminer X et Y en fonction de x et y.
b)déterminer l'ensemble E des points M d'affixe z tels que Z soit réel.
c)déterminer et construire l'ensemble F des points M d'affixe z tels que Z soit imaginaire pur.



merci d'avance pour l'aide que vous pourrez m'apporter.
guillaume8

[becirj]

Bonjour
1. Il faut remplacer z par puis obtenir la réponse sous forme algébrique en multipliant numérateur et dénominateur par le conjugué du dénominateur.

2. On résout l'équation Z=z soit qui se ramène à une équation du second degré.

3. Un module est une distance : ,
Le module d'un quotient est égal au quotient des modules.

Voila de quoi démarrer, on verra pour la suite.

[Anonyme]

déja, merci pour cette petite aide!
j'ai donc réussi à faire le début de l'exercice...
pour le 1) j'ai trouvé 2+i(racine de 2) comme affixe de C'=f(C)
pour le 2) j'ai trouvé l'affixe de I (1+i(racine de 2)) et l'affixe de J (1-i(racine de 2))
mais, dés la question 3), je rebloque...
d'après ce que vous m'avez dit, j'ai mis que |Z|=OM' , que |z-4|=BM et que |z-1|=AM
mais à partir de la 2ème partie de cette question : En déduire l'ensemble D des points M d'affixe z tels que |Z|=1 .... je n'arrive pas du tt à trouver l'ensemble D ....

et puis après, pour la question 4), j'ai essayé de continuer, mais je ne sais pas si je pars dans la bonne direction...
puisque Z=X+iY , z=x+iy et Z=(z-4)/(z-1) , j'ai essayé de remplacer les termes. ce qui me donne X+iY=(x-4+iy)/(x-1+iy) ... mais après, je ne vois pas comment trouver X et Y en fonction de x et y ...


donc je vous remercie pour l'aide que vous pourrez m'apporter!
guillaume8

[becirj]

Bonjour et bon Noël
2. Je n'ai pas obtenu les mêmes réponses.
J'ai comme équation :


3. Le module d'un quotient est égal au quotient des modules, donc
équivaut à BM=AM.
L'ensemble des points M tels que BM=AM est la médiatrice D de [A,B].
On a alors OM'=1 donc M' appartient au cercle de centre O et de rayon 1.

4.a) Pour obtenir X et Y , il faut écrire le quotient sous forme algébrique en multipliant numérateur et dénominateur par le conjugué du dénominateur en distinguant bien partie réelle et partie imaginaire.


On a donc : et
b) Z est réel si sa partie imaginaire est nulle soit soit 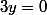et soit
L'ensemble E est donc l'axe des abscisses privé du point A d'affixe 1.
c) Z est imaginaire pur si sa partie réelle est nulle soit et
est le début du développement d'un carré : celui de


On reconnaît l'équation d'un cercle. L'ensemble F est le cercle de centre le point de coordonnées et de rayon privé du point A d'affixe 1.

Cet exercice est très classique, essaie de bien voir les méthodes, tu les retrouveras souvent.

[Anonyme]

ben merci beaucoup! j'ai enfin compris! ^^

2. Je n'ai pas obtenu les mêmes réponses.
J'ai comme équation :

et pour ça, autant pour moi! je m'étais trompé de ligne! :p j'avais effectivement trouvé cela!