Complexes : ensemble de points
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 06:16
par sue » 07 Nov 2006, 06:16
bonjour,
j'arrive pas à déterminer l'ensemble de point M t.q :
 = Im(z^3))
avec
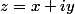
.
j'arrive jusqu'ici mais je vois pas ce que ça donne :

j'ai besoin juste d'un indice
MERCI
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 06:43
par sue » 07 Nov 2006, 06:43
bon je trouve qq chose je crois que c'est bon ...
c'est l'union de la droite d'équation x= -y et le cercle de centre o(1,1) et de rayon

.
ect-ce juste ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 07 Nov 2006, 07:47
par Zebulon » 07 Nov 2006, 07:47
Bonjour,
sue a écrit: j'arrive pas à déterminer l'ensemble de point M t.q :
 = Im(z^3))
avec
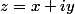
.
j'arrive jusqu'ici mais je vois pas ce que ça donne :

en calculant avec la forme algébrique, je trouve
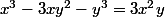
.
Mais je ne pense pas que ce soit la bonne méthode. C'est plus simple avec la forme exponentielle :
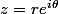
donc
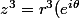^3=r^3e^{3i\theta})
. Que valent alors
)
et
)
?
Donc
=Im(z^3)\ \Longleftrightarrow\ ...)
?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 08:14
par sue » 07 Nov 2006, 08:14
re,
j'ai pas encore vu la forme exponentielle mais voilà ce que je trouve avec la forme algébrique :
 (x^2 +y^2 -xy -3xy ) = 0 \; \Leftrightarrow \; x=-y \; ou \; (x-1)^2 + (y-1)^2 = 2)
donc je j'ai dit est juste je crois ?
j'aimerais que tu m'explique ta méthode car peut etre on va la voir aujourd'hui .
merci :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 07 Nov 2006, 08:14
par Zebulon » 07 Nov 2006, 08:14
Pardon, vous aviez raison, c'est bien
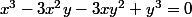
.
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 08:21
par sue » 07 Nov 2006, 08:21
ok , pouvez-vous me dire comment on fait avec l'exponentielle , j'ai lancé un coup d'oeil sur mon livre et je peux dire que ce que vous m'avez dit équivaut à :
 = r^3 sin(3\theta))
non ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 07 Nov 2006, 08:39
par Zebulon » 07 Nov 2006, 08:39
sue a écrit:  (x^2 +y^2 -xy -3xy ) = 0 \; \Leftrightarrow \; x=-y \; ou \; (x-1)^2 + (y-1)^2 = 2)
Je suis d'accord que c'est équivalent à
(x^2+y^2-xy-3xy)=0)
donc équivalent à
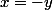
ou
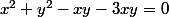
.
Mais
^2+(y-1)^2=2\ \Longleftrightarrow\ x^2-2x+y^2-2y=0)
ce qui n'est pas équivalent à
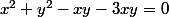
.
Dommage, c'était très bien vu !
Pour l'exponentielle, c'est bien ça :
=Im(z^3)\ \Longleftrightarrow\ r^3cos(3\theta)=r^3sin(3\theta))
.
Distinguez les cas
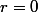
et

et posez
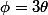
.
P.S.: Si vous n'avez pas vu la forme exponentielle, vous pouviez obtenir le même résultat avec
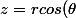+irsin(\theta))
où r est le
module de z (

) et

est l'
argument de z (
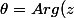)
).
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 08:51
par sue » 07 Nov 2006, 08:51
j'ai meme pas vu la forme trigonométrique , on a juste vu la forme algébrique ... :triste:
merci pour tt , je dois quitter maintenant je verrai plus tard comment je peux m'ensortir ..
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 07 Nov 2006, 08:54
par Zebulon » 07 Nov 2006, 08:54
Zebulon a écrit:=Im(z^3)\ \Longleftrightarrow\ r^3cos(3\theta)=r^3sin(3\theta))
.
Distinguez les cas
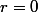
et

et posez
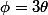
.
Arrivé là, ce n'est plus difficile. Moins que de trouver des factorisations comme vous l'avez fait !
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 09:41
par sue » 07 Nov 2006, 09:41
re,
une séance des maths ratée

, je reviens sur cet exo ..
si
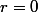
on a
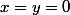
(je crois ) donc l'ensemble de points est o(0,0)
si
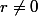
alors
 = sin(3\theta) \Leftrightarrow ; tan(3\theta) = tan(\frac{\pi}{4}) \Leftrightarrow \; \theta = \frac{\pi}{12} + \frac{\pi}{3} k \;\;donc\;\; arg(z) \equiv \frac{\pi}{12} [\frac{\pi}{3}])
je crois pour que ça soit vrai il faut que

désolée si je raconte des horreurs j'ai pas encore vu ça :triste:
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 09:48
par sue » 07 Nov 2006, 09:48
bon je dois partir avant de rater une autre séance ...
@+
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Nov 2006, 14:21
par sue » 07 Nov 2006, 14:21
bon personne pour m'aider ?! :triste:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 07 Nov 2006, 17:42
par Zebulon » 07 Nov 2006, 17:42
sue a écrit:donc
 \equiv \frac{\pi}{12} [\frac{\pi}{3}])
Oui c'est bien.
Si on appelle S l'ensemble solution, on a :
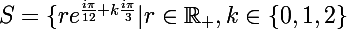
Je vous laisse simplifier.
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 08 Nov 2006, 20:45
par sue » 08 Nov 2006, 20:45
re,
merci beacoup Zebulon ..mais je vois pas pourquoi vous choisissez

et je vois pas encore comment peut-on en déduire l'ensemble de points , ça m'a pas l'air si evident avec ce petit e .:triste:
pouvez-vous m'expliquer svp ?
merci :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 08 Nov 2006, 21:22
par Zebulon » 08 Nov 2006, 21:22
Zebulon a écrit:Oui c'est bien.
Si on appelle S l'ensemble solution, on a :
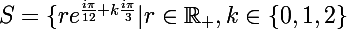
Je vous laisse simplifier.
Je me suis trompée, c'est

.
Vous êtes d'accord que
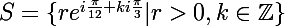
? Si oui, il suffit alors de montrer que
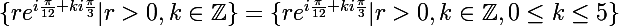
.
Preuve :
On a le sens
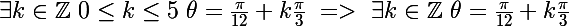
qui est évident donc

et dans l'autre sens,
si

tel que
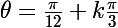
, alors on prend le reste de k modulo 6 :

tel que
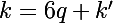
donc
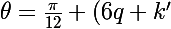{\pi\over3}={\pi\over12}+2q\pi+k'{\pi \over3})
donc
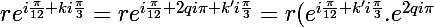=re^{i{\pi \over 12}+k'i{\pi \over3}})
ce qui montre que

donc
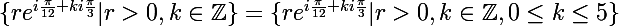
d'où
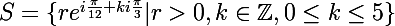
.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 08 Nov 2006, 21:26
par Zebulon » 08 Nov 2006, 21:26
Zebulon a écrit: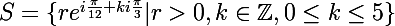
.
En réalité, quand on les calcule tous, on s'aperçoit que
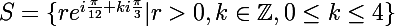
.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 09 Nov 2006, 00:15
par rene38 » 09 Nov 2006, 00:15
Bonsoir
On remarque aussi que pour k=3 et k=4 on retrouve à

près les valeurs d'angle polaire obtenues avec k=0 et k=1 respectivement.
et si on revient à l'écriture algébrique,

s'écrit aussi

qu'on peut considérer comme une équation d'inconnue

et qui donne :

qui sont les équations de
3 droites qui passent par l'origineet qui font avec l'axe réel des angles de

(tout ça modulo

) et qui constituent l'ensemble cherché.
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 09 Nov 2006, 00:26
par sue » 09 Nov 2006, 00:26
Ah wé c'est trés clair :+++:
merci beaucoup à vous deux ..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
avec
.

 (x^2 +y^2 -xy -3xy ) = 0 \; \Leftrightarrow \; x=-y \; ou \; (x-1)^2 + (y-1)^2 = 2)
 s'écrit aussi
s'écrit aussi


 (tout ça modulo
(tout ça modulo  ) et qui constituent l'ensemble cherché.
) et qui constituent l'ensemble cherché.