Complexe

par **ultas** » 19 Jan 2009, 14:11

Bonsoir a tous j'aurai besoin de votre aide pour cette exercice.
Alors on a une application f qui a tout point M d'affixe z non nulle associe le point M'=f(M) d'affixe z' tel que [TEX]z'=/frac{z}{mod(z)}*(2-[z])[/TEX ] avec [z] qui signifie module ou valeur absolue de z .On a aussi z=r*e^ia r etant le module de z et a un argument de z.On a aussi [TEX] z'=e^{2-r}[TEX ]
De plus on a pour cette question un point M du plan a l'exterieur du cercle de rayon 1 .On appelle I le milieu du segment [MM'] ou M' est l'image de M par f .
Il faut montrer que I appartient au cercle C1 de rayon 1 et a la demi-droite [OM) J'ai essaye de repondre mais je n'ai pas compri ou serait le point M' j'espere que vous pourrez m'aider merci a tous

par **XENSECP** » 19 Jan 2009, 14:16

Rends ça digeste et je le lirais ^^

par **axiome** » 19 Jan 2009, 14:16

Bonjour,
Ton cercle de rayon 1, c'est quoi son centre ?

par **ultas** » 19 Jan 2009, 14:17

c l'origine 0

par **axiome** » 19 Jan 2009, 14:18

XENSECP a écrit:Rends ça digeste et je le lirais ^^

C'est vrai que c'est pas très bon pour la digestion quand on sort de table...
:ptdr:

Regarde ici, c'est très bien fait...

par **ultas** » 19 Jan 2009, 14:25

jespere que mais changement sur l'enoncé vous plairons

par **axiome** » 19 Jan 2009, 14:26

ultas a écrit:jespere que mais changement sur l'enoncé vous plairons

Pas tellement si tu ne mets pas entre balise [TEX]...
:we:

par **ultas** » 19 Jan 2009, 14:31

e maintenant??

par **axiome** » 19 Jan 2009, 14:33

f est une application qui a tout point M d'affixe z non nulle associe le point M'=f(M) d'affixe z' tel que :

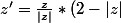On a aussi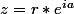

r étant le module de z et a un argument de z.
On a aussi

De plus, on a, pour cette question un point M du plan a l'extérieur du cercle de centre 0 et de rayon 1. On appelle I le milieu du segment [MM'] ou M' est l'image de M par f .
Il faut montrer que I appartient au cercle C1 de rayon 1 et a la demi-droite [OM).

par **axiome** » 19 Jan 2009, 14:34

Dis-moi si j'ai bien recopié l'énoncé...

par **ultas** » 19 Jan 2009, 14:35

oui c exactement ca

par **axiome** » 19 Jan 2009, 14:37

Alors, donne nous l'affixe de I sachant que c'est le milieu de [MM'].

par **ultas** » 19 Jan 2009, 14:39

l'affixe de I c'est la somme de l'affixe de M et de M' divisé par 2

par **axiome** » 19 Jan 2009, 14:42

J'ai répondu par message privé.

par **ultas** » 19 Jan 2009, 14:46

je n'ai pas compris votre reponse

par **axiome** » 19 Jan 2009, 14:47

Les messages privés sont en haut à droite de la fenêtre.

par **ultas** » 19 Jan 2009, 14:49

moi osssi g mm plus de temp g cours encore merci pour votre aide.

Complexe

complexe

Qui est en ligne