Complexe

[ptitmatteo]

bonjour voila mon sujet c'est un exercice que j'ai eu dans mon livre ses juste pour bien mentrainer pour le bac blanc pour moi la semain prochain donc je veu me remettre au point sur les complexes:


voila pour la 1. dite mois si cela est juste
1.
z²+8z+17=0
= 8² – 4*1*17 = - 4

x1=( -8 + i;)4 )/( 2*1) = (-8 + 2i) / 2= - 4 + i
x2=( -8 – i;)4 )/( 2*1) = (-8 – 2i ) / 2= - 4 – i

l'équation a pour solution -4 + i et -4 – i

[maf]

J'ai la même chose que toi pour la 1)

[Le Yaude]

J'ai pareil aussi pour la 1

[ptitmatteo]

2.
(z – 6)(z² + 8z+ 17)
on dévellope:
z³ + 8z² + 17z – 6z² – 48z + 102
z³ + 2z² – 31z +102
alors
P(z)=(z – 6)(z² + 8z+ 17)= z³ + 2z² – 31z +102

es que c'est juste

[maf]

2) d'après moi c'est bon ...

Ou alors tu peux vérifier que z=6 est solution puis procéder à la division euclidienne

[ptitmatteo]

3.
on sait que:
P(z) = (z – 6)(z² + 8z+ 17) = z³ + 2z² – 31z +102
et
z² + 8z + 17 = 0
x1 = -4 + i
x2 = -4 – i

z – 6 = 0
z = 6
donc
P(z) a pour S={-4 + i ;-4 – i ;6 }

et là toujour juste???

[maf]

toujours d'après moi ...

[ptitmatteo]

parcontre pour la 1 de la b
je ne csais pas comment faire je sais que sais symétrique mais je ne sais pas comment rédiré é justifier

[maf]

Apparemment on te demande les normes des vecteurs OB et OB' ...

donc .. utilise Pythagore

[ptitmatteo]

pk pytagore car nous on na ke 2 vecteur pas de triangle

[maf]

un complexe s'écrit z = a + ib

le module de z (la norme de 0 au point z) = racine carrée de (a^2+b^2)

Ce qui est l'utilisation de pythagore

Montre simplement qu'ils ont le même module

[ptitmatteo]

alors la je n'ai absolument rien compris
il na pas plus simple par hazar

[Yawgmoth]

Yo, voici les "réponses" du 1. partie B.

1.b. Comme l'a dit maf (béni soit-il :happy2: ) il faut vérifier que B et B' ont même module. Comme ils ont pour origine commune ... l'origine du repère du plan de Gauss, c'est bon faut pas aller plus loin.

1.c. Il faut se rappeler de ce petit truc pour la "transformation" d'un nombre complexe qui est sous forme de fraction en forme algébrique. Je te file la règle générale, tu adapteras ensuite à ton calcul (à ce que j'ai compris faut que tu pratiques :marteau: ). . Or est un réel donc tu réarranges le tout pour obtenir ton nombre complexe sous la forme .

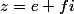
1.d. Une fois que t'as trouvé l'écriture algébrique, pour le module c'est facile, suffit d'appliquer la formule.
Pour l'argument, il faut se servir de la règle comme quoi le cosinus de l'argument = la partie réelle du nombre complexe divisée par son module. Pour vérifier, tu peux aussi utiliser le sinus de l'argument = la partie imaginaire (NE PAS NOTER i) du nombre complexe divisée par son module.

Voilà l'écriture mathématique de tout ce blabla :
Supposons le nombre complexe z = a + bi. Notons son argument et son module .

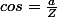
et .

1.e. Bon alors là, il faut utiliser la représentation de Gauss (si tu sais plus ce que c'est, va vite sur Wikipédia). Une fois que tu auras représenté OB et OB', ton triangle t'apparaîtra et là, tu utilises l'argument que tu as trouvé précédemment.


J'espère que ce n'est pas trop embrouillé :mur:

[ptitmatteo]

1.b
on sait b est b' son symétrique par rapport a l'axe de abscisse est on sait qui on un module opposer
donc 0b=0b'
c.
(-4 + i)/(-4 – i)
(-4 + i)(-4 + i) /(-4 – i)(-4 + i)
(16 – 4i – 4i + 1)/(4² – i²)
(17 – 8i )/(16 + 1)
(17 – 8i )/17
1 – 8i/17

jusque la c'est juste et bien ridiger

[Yawgmoth]

Attention, t'as fait une petite erreur pour le 1.c

Tu as écrit (-4 + i)(-4 + i) = (16 – 4i – 4i + 1)

La réponse est (-4 + i)(-4 + i) = (16 – 4i – 4i + (i . i)) or (i.i) = i^2 vaut - 1 et non + 1

Du moins j'espère ... :mur: :mur:

[ptitmatteo]

c.
(-4 + i)/(-4 – i)
(-4 + i)(-4 + i) /(-4 – i)(-4 + i)
(16 – 4i – 4i – 1)/(4² – i²)
(15 – 8i )/(16 + 1)
(15 – 8i )/17
et la c mieu???
et pour la question b si je mais que sa il me conte pas faut?

[Yawgmoth]

Désolé, je voulais pas t'offenser en relevant ton erreur :briques: :briques: désolé si j'ai pu paraître désagréable :cry: .

Pour vérifier l'égalité de deux nombres complexes, il y a deux choses :

- il faut que leurs modules soient égaux
- il faut que la valeur absolue de leurs arguments soit égale.

[ptitmatteo]

mais mes calcule sont juste
je en vois pas mon erreur

[Yawgmoth]

Ton erreur ? Elle peut pas provenir du 1.c il est juste.

[ptitmatteo]

Je pense que c'est tout mais y a un truc qui me chiffonne quant à l'argument ... problème de signes :mur:

c a dire !!!