Complexe et géométrie

par **MRSmystère** » 03 Oct 2012, 17:19

Bonjour,

J'aimerai de l'aide pour la question 2 de cette exercice,
Si vous avez besoin des réponses des premières questions, je vous les donnerai.

[img][img]http://nsa30.casimages.com/img/2012/10/03/mini_121003063223295740.jpg[/img][/IMG]

Merci de votre aide.

par **tototo** » 03 Oct 2012, 17:56

MRSmystère a écrit:Bonjour,

J'aimerai de l'aide pour la question 2 de cette exercice,
Si vous avez besoin des premières questions, je vous les donnerai.

[img][img]http://nsa30.casimages.com/img/2012/10/03/mini_121003063223295740.jpg[/img][/IMG]

Merci de votre aide.

Bonjour,

A,B,C sont sur le cercle car Aomega=racine(25)=5 car A=a1+ia2 B=b1+ib2 AB=racine((a1-b1)^2+(a2-b2)^2)
Bomega=racine(16+9)=5
Comega=racine(9+16)=5
donc A,B,C sont sur le cercle .

par **MRSmystère** » 03 Oct 2012, 18:00

Merci, mais ce n'était pas la question qui me pose problème, au moins je sais que c'est bon,
Mais je parlais de la question 2) À tout point M du plan ... ^^

par **Skare** » 03 Oct 2012, 18:14

? on vois mal.

soit

avec

arg (kz)= arg(z)

donc

donc O,M et M' sont alignés.

par **MRSmystère** » 03 Oct 2012, 18:40

Skare a écrit: ? on vois mal.

soit

avec

arg (kz)= arg(z)

donc
donc O,M et M' sont alignés.

Oui c'est bien cette énoncé, j'ai bien commencé comme vous en utilisant l'écriture algébrique mais je ne comprends pas très bien le raisonnement après le k.z pour montrer l'alignement des points

Merci de votre aide ^^

par **Anonyme** » 03 Oct 2012, 20:07

On a

avec

Ce qu'il faut comprendre c'est que :
k est un nombre réel ( peu importe qu'il soit positif on négatif)

Comme

on dit que ces 2 vecteurs sont colinéaires

et donc les points O , M d'affixe z , et M' d'affixe z' sont alignés

par **MRSmystère** » 03 Oct 2012, 21:41

ptitnoir a écrit:On a
avec

Ce qu'il faut comprendre c'est que :
k est un nombre réel ( peu importe qu'il soit positif on négatif)

Comme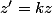 on dit que ces 2 vecteurs sont colinéaires

et donc les points O , M d'affixe z , et M' d'affixe z' sont alignés

Mais oui ! Merci beaucoup à vous deux et une dernière question vous auriez une piste à me souffler pour la. 3) b) ?

par **Anonyme** » 03 Oct 2012, 22:00

La question 3.b) n'est pas difficile
car tu connais z' en fonction de z (barre)

donc
1) tu peux calculer z' (barre) en fonction de z

2) puis tu peux répondre à ta question 3.b

par **MRSmystère** » 03 Oct 2012, 22:17

ptitnoir a écrit:La question 3.b) n'est pas difficile
car tu connais z' en fonction de z (barre)

donc
1) tu peux calculer z' (barre) en fonction de z

2) puis tu peux répondre à ta question 3.b

Bien-sûr ! Merci beaucoup et bonne nuit :-)

Complexe et géométrie

Complexe et géométrie

Qui est en ligne