Complexe affixe vérification

par **chuchi** » 26 Déc 2008, 01:51

bonsoir,

ya quelques truc que je comprend pas (disons qui ne sont pas détaillés dans mon cours) et j'aimerais juste que vous vérifiez pour voir si j'ai compris ; je vais illustrer avec un exemple :

soit M d'affixe z, on associe le point M' d'affixe z' =

Calculer l' affixe de A' de A (-3;4)

pour A'

zA = -3 + 4i

zA' =

zA' =

et la je peux conclure?? ou je dois multiplié par la partie conjugué? (j'opterais pour ça) et donc :

zA' =

zA' =

*

zA' =

+i

d'ou A' (

;

)

par **fatal_error** » 26 Déc 2008, 02:22

Salut,

Vi, le raisonnement est bon.
Pour vérifier, tu peux utiliser ta solution trouvée et reporter dans ta première équation, pour voir si tu trouves bien la même choses des cotés des deux membres.

Genre z' solution =>

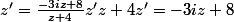
et developper pour vérifier

par **chuchi** » 26 Déc 2008, 03:18

excuse moi mais afin d'etre sur d'avoir parfaitement compris, ça donnerais :

zA'zA + 4zA' = -3i(zA) + 8

et la on remplace zA et zA' ?

par **fatal_error** » 26 Déc 2008, 11:08

vi, normalement, tu dois trouver la même chose (même partie imaginaire et même partie réelle) a gauche et a droite.

par **chuchi** » 26 Déc 2008, 18:22

mais un autre truc comment trouver z (je reprends le méme exemple) :

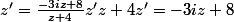
quand on a ça, on repart de

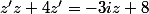
et pour trouver z, comment faut -il isoler??

par **xyz1975** » 26 Déc 2008, 18:28

Que cherches-tu?

par **chuchi** » 26 Déc 2008, 20:43

xyz1975 a écrit:Que cherches-tu?

a comment trouver z connaissant z', à isoler z quoi

par **chuchi** » 26 Déc 2008, 23:03

a comment trouver z connaissant z', à isoler z quoi

par **chuchi** » 27 Déc 2008, 02:46

a comment trouver z connaissant z', à isoler z quoi

par **chuchi** » 27 Déc 2008, 14:49

up svp , j'ai tjs pas compris :s

par **chuchi** » 27 Déc 2008, 21:11

up svp , j'ai tjs pas compris :s

par **chuchi** » 27 Déc 2008, 22:41

up svp , j'ai tjs pas compris :s

par **XENSECP** » 27 Déc 2008, 22:51

chuchi a écrit:Calculer l' affixe de A' de A (-3;4)

pour A'

zA = -3 + 4i

zA' =
zA' =
zA' = ERREUR DE SIGNE

Bon ba recommence les calculs ^^

par **XENSECP** » 27 Déc 2008, 22:53

chuchi a écrit:Calculer l' affixe de A' de A (-3;4)

pour A'

zA = -3 + 4i

zA' =
zA' =
zA' =

Voilà où est l'erreur

Il n'y a 12i mais juste 12

par **chuchi** » 27 Déc 2008, 23:05

XENSECP a écrit:Voilà où est l'erreur
Il n'y a 12i mais juste 12

oui merci j'avais pas vu mais aussi, pour un autre truc ;

imaginons que j'ai :

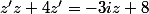
connaisant z' comment fais je à retrouver z, je n'arrive pas à isoler

par **pgeod** » 27 Déc 2008, 23:15

z'z + 4z' = -3iz + 8
<=> z'z + 3iz = -4z' + 8
<=> z (z' + 3i) = -4z' + 8
............ si z' /= -3i
<=> z = (-4z' + 8) / (z' + 3i)

...

par **chuchi** » 28 Déc 2008, 00:38

merci!! ct pas dur :s

par **chuchi** » 28 Déc 2008, 00:53

merci j'avais pas fais attention ...

et de ce genre comment faire :

(z-3)(z') = 3i(z)-6

par **Huppasacee** » 28 Déc 2008, 00:58

(z-3)(z') = 3i(z)-6

retrouve :

z ( cz' + d) = az' + b

par **chuchi** » 28 Déc 2008, 01:24

mais c pas logique, ya que 2 z et un z' et le -3 dans (z-3) me géne :s

Complexe affixe vérification

complexe affixe vérification

Qui est en ligne