Le compas

[magma58]

Les deux extrémités et le point d'articulation des branches d'un compas forment un triangle.

Existe-t-il un écartement des branches pour lequel l'aire de ce triangle est maximale ?

Je ne vois comment convertir ce problème en équation .....

Merci de bien vouloir m'aider

[Dr Neurone]

Les deux extrémités et le point d'articulation des branches d'un compas forment un triangle.

Existe-t-il un écartement des branches pour lequel l'aire de ce triangle est maximale ?

Je ne vois comment convertir ce problème en équation .....

Merci de bien vouloir m'aider

Bonsoir , en forme?

[Eva77]

Oula. Sa me dit quelque chose que mon frère avait fait.
Je vais lui en parler .

[zenaf]

en fait, tu exprimes chacun de tes coté selon l'angle alpha. De ces cotés, t'en conclu une expression de l'aire du triangle et tu fera une optimisation (par dérivé de ta fonction donnant l'aire)

[dudumath]

Un petit indice ton triangle est un triangle équilatéral.
Bonne chance pour la suite

[magma58]

comment faire pour exprimer les côtés en fonction de l'angle alpha alors que le triangle n'est pas rectangle et qu'on ne connaît pas la mesure de l'angle...

===> peux-tu m'expliquer rapidemant ce qu'est une dérivée stp ( on a pas encore vu ça en cours)

merci beaucoup

[flight]

...non le triangle est isocèle , 2 cotés isometriques qui représentent les branches du compas .

soit µ l'angle au sommet , alors l'aire fonction de µ pour le triangle ainsi formé est A(µ)= (L².sinµ) /2 il suffit de dériver cette fonction et de chercher pour quelle valeur de µ A'(µ) s'annulle et calculer ensuite son image par A(µ)

[rene38]

Bonsoir

Un petit indice ton triangle est un triangle équilatéral.Bonne chance pour la suite

Tu es certain ? Moi j'en doute fort.

[rene38]

soit µ l'angle au sommet , alors l'aire fonction de µ pour le triangle ainsi formé est A(µ)= (L².sinµ) /2 il suffit de dériver cette fonction et de chercher pour quelle valeur de µ A'(µ) s'annulle et calculer ensuite son image par A(µ)

A(µ)= (L².sinµ) /2 : la seule variable est µ. Il est donc inutile de dériver : A(µ) est maximale lorsque sin(µ) est maximal : égal à 1 et donc lorsque µ=pi/2 .
Le triangle est alors isocèle et rectangle et l'aire vaut L²/2.

[magma58]

merci beaucoup ^^
j'aimerais juste une petite explication de ce qu'est une dérivée svp

[Imod]

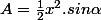
En notant la taille des branches du compas et l'angle entre les branches , le reste est facile .

Imod

EDIT : grillé par rene :marteau:

[magma58]

oki merci beaucoup tout le monde juste une dernière précision car j'ai bien séparé le triangle en 2 triangles isométriques mais pour moi il y a 3 côtés inconnus et pour exprimer l'aire, il faut utiliser le cosinus de l'angle.... :mur:

merci de m'éclairer un peu....^^

[magma58]

vous pouvez détailler comment vous trouver cette expression car j'ai compris le principe mais vous exprimez le sinus de l'angle alpha alors que le triangle n'est pas rectangle...