Comparer x et x^3
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Thoulia
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Nov 2011, 13:07
-
 par Thoulia » 26 Nov 2012, 21:17
par Thoulia » 26 Nov 2012, 21:17
bonjours j'aurais besoin d'un petit coup de main s'il vous plait :
comment peut on comparer x et x^3 pour x dans une intervalle de (0:+infini(
je sais que ça reviens tout d'abord à comparer A-B donc x-x^3 mais ensuite ?
Merci d'avance XD
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 26 Nov 2012, 21:20
par mcar0nd » 26 Nov 2012, 21:20
Thoulia a écrit:bonjours j'aurais besoin d'un petit coup de main s'il vous plait :
comment peut on comparer x et x^3 pour x dans une intervalle de (0:+infini(
je sais que ça reviens tout d'abord à comparer A-B donc x-x^3 mais ensuite ?
Merci d'avance XD
Salut, bonne idée d'utiliser la différence.

Maintenant, il faut que tu factorise

.

-
Thoulia
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Nov 2011, 13:07
-
 par Thoulia » 26 Nov 2012, 21:27
par Thoulia » 26 Nov 2012, 21:27
mcar0nd a écrit:Salut, bonne idée d'utiliser la différence.

Maintenant, il faut que tu factorise

.

ce qui reviens à dire :
x-x*x*x*1= x(x-1)
??????
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 26 Nov 2012, 21:29
par mcar0nd » 26 Nov 2012, 21:29
Thoulia a écrit:ce qui reviens à dire :
x-x*x*x*1= x(x-1)
??????
Alors plus simplement,
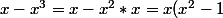)
.

-
Thoulia
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Nov 2011, 13:07
-
 par Thoulia » 26 Nov 2012, 21:36
par Thoulia » 26 Nov 2012, 21:36
mcar0nd a écrit:Alors plus simplement,
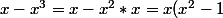)
.

ah ok , merci beaucoup !!!^^
mais ça marchait sinon pour l'autre
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 26 Nov 2012, 21:38
par mcar0nd » 26 Nov 2012, 21:38
Thoulia a écrit:ah ok , merci beaucoup !!!^^
mais ça marchait sinon pour l'autre
Non, c'est faux ce que tu avais mis.
Pour t'en rendre compte, il suffit de développer,
=x*x-x*1=x^2-x)
-
Thoulia
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Nov 2011, 13:07
-
 par Thoulia » 26 Nov 2012, 21:43
par Thoulia » 26 Nov 2012, 21:43
mcar0nd a écrit:Non, c'est faux ce que tu avais mis.
Pour t'en rendre compte, il suffit de développer,
=x*x-x*1=x^2-x)
merci merci ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
