Comparer 2 nombres

[so213]

Bonjour j'ai une question d'un dm qui me pose problème je vous explique.
f est une fonction définit sur l'intervalle [-1;+l'infini[ par f(x)=racine de 1+x
question 1 :
a)Sur cette intervalle comparez les nombres racine de 1+x et 1+x/2

[Carpate]

Bonjour j'ai une question d'un dm qui me pose problème je vous explique.
f est une fonction définit sur l'intervalle [-1;+l'infini[ par f(x)=racine de 1+x
question 1 :
a)Sur cette intervalle comparez les nombres racine de 1+x et 1+x/2

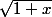
Est-ce comparer et
ou
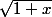
comparer et
ou encore
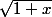
comparer et ?
Ah, les parenthèses ...

[so213]

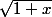
Est-ce comparer et
ou
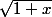
comparer et
ou encore
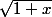
comparer et ?
Ah, les parenthèses ...

La première proposition

[Carpate]

La première proposition

Cherche le signe de

[so213]

Cherche le signe de

Le tableau de signe ? Oui j'ai pensé à ça mais je bloque sachant que 1+(x/2) est un quotient

[Carpate]

Le tableau de signe ? Oui j'ai pensé à ça mais je bloque sachant que 1+(x/2) est un quotient

Non, pense à la quantité conjuguée
Le résultat est immédiat

[so213]

Non, pense à la quantité conjuguée
Le résultat est immédiat

Pourrais tu m'éclairer à propos de la quantité conjuguée stp parce que je suis un peu perdue :triste:

[chan79]

a)Sur cette intervalle comparez les nombres racine de 1+x et 1+x/2

1+x doit être positif

tu peux comparer sur

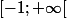
Ensuite, tu peux comparer les carrés

[Carpate]

Pourrais tu m'éclairer à propos de la quantité conjuguée stp parce que je suis un peu perdue :triste:

On ne sait pas établir rapidement le signe de
Mais en mutipliant cette expression par sa quantité conjuguée : en haut et en bas ce qui ne change pas la valeur de l'expression:

et en utilisant une identité remarquable au numérateur, cela se simplifie pas mal ...

[so213]

On ne sait pas établir rapidement le signe de
Mais en mutipliant cette expression par sa quantité conjuguée : en haut et en bas ce qui ne change pas la valeur de l'expression:

et en utilisant une identité remarquable au numérateur, cela se simplifie pas mal ...

D'accord, je vois mais à la fin après avoir appliquer l'identité remarquable, en ce qui concerne le dénominateur j'ai toujours une racine carrée et un quotient

[so213]

j'obtiens (1+x)-(1+(x/2))^2 / (racine(1+x) + (1+(x/2)))

[Carpate]

D'accord, je vois mais à la fin après avoir appliquer l'identité remarquable, en ce qui concerne le dénominateur j'ai toujours une racine carrée et un quotient

Tu n'as plus de racine carrée au numérateur (c'était le but de la manip) mais seulement au dénominateur et ce dénominateur est positif sur
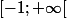
Que trouves-tu au numérateur ?

[so213]

Tu n'as plus de racine carrée au numérateur (c'était le but de la manip) mais seulement au dénominateur et ce dénominateur est positif sur
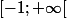
Que trouves-tu au numérateur ?

Je trouve racine carrée(1+x) + (1+x/2)

[Carpate]

Je trouve racine carrée(1+x) + (1+x/2)

Mais non
Il s'agit du numérateur de
soit
de la forme

Tu vois bien que la racine carrée disparait

[so213]

Mais non
Il s'agit du numérateur de
soit
de la forme

Tu vois bien que la racine carrée disparait

Ha oui voilà j'avais trouvé ça :++: sauf que j'ai été étourdie je pensais que vous me demandiez le dénominateur :ptdr: donc du coup maintenant le numérateur va me servir à faire mon tableau de signe et le dénominateur étant positif et compris dans l'intervalle on en a plus besoin, c'est bien ça ? :hein:

[Carpate]

Ha oui voilà j'avais trouvé ça :++: sauf que j'ai été étourdie je pensais que vous me demandiez le dénominateur :ptdr: donc du coup maintenant le numérateur va me servir à faire mon tableau de signe et le dénominateur étant positif et compris dans l'intervalle on en a plus besoin, c'est bien ça ? :hein:

Et le numérateur est particulièrement simple : dont le signe ne devrait pas être difficile à établir ..

[so213]

Et le numérateur est particulièrement simple : dont le signe ne devrait pas être difficile à établir ..

Le numérateur je trouve (1+x)(-x^2/4) , c'est factorisé donc je peux commencer à faire mon tableau de signe ?

[Carpate]

Le numérateur je trouve (1+x)(-x^4) , c'est factorisé donc je peux commencer à faire mon tableau de signe ?

Le numérateur est :

[so213]

Le numérateur est :

Oui , c'est bon j'ai refais mon calcul et j'ai trouvé comme toi, je peux enfin faire mon tableau de signe :id: Merci bcp de m'avoir aidé :++:

[zygomatique]

salut

pour comparer deux nombres positifs on peut comparer leur carrés !!!

:mur:

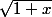
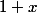
donc comparer les nombres et équivaut à comparer les nombres et

justifier évidemment l'équivalence ....

:ptdr: