Bonjour à tous,
J'ai un DM à rendre pour dans 2 jours et je ne comprends pas comment m'y prendre pour le faire et surtout avoir une bonne note (ce qui pourrait faire remonter ma moyenne de maths). Merci d'avance aux personnes qui me répondront.
Voici le sujet :
Soient x et y deux réels strictement positifs. On définit leurs moyennes arithmétique, géométrique et harmonique par les formules :
a=1/2(x+y) g=√xy 1/h=1/2(1/x+1/y)
1)Montrer que ∀ x,y ∈ R+∗ h ≤ g ≤ a
2)Montrer que ces trois moyennes sont comprises entre x et y
DM Comparer des moyennes
7 messages
- Page 1 sur 1
Re: DM Comparer des moyennes
Bonsoir,
Commence par calculer h.
Ensuite pose les inégalités à démontrer et procède par équivalence.
Remarque: a = sqrt(a)**2
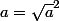
Commence par calculer h.
Ensuite pose les inégalités à démontrer et procède par équivalence.
Remarque: a = sqrt(a)**2
Modifié en dernier par mathelot le 16 Nov 2021, 21:10, modifié 1 fois.
Re: DM Comparer des moyennes
re,
en généralisant comme moyennes de n nombres strictement positifs:
strictement positifs:
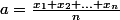
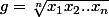
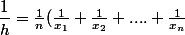)
a-t-on toujours ?
?
remarque: pour les dix nombres de 1 à 10,on obtient:
a=5,5 ; g=4,528728688 , h=3,414171521
en généralisant comme moyennes de n nombres
a-t-on toujours
remarque: pour les dix nombres de 1 à 10,on obtient:
a=5,5 ; g=4,528728688 , h=3,414171521
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
