La comparaison

[zahira]

Bonjour
Soit x appartient a R comparer


Et

Modifié par Lostounet

[Lostounet]

Salut j'ai modifié ton message pour le rendre plus lisible

[Grizet]

Salut, tu peux noter la première fonction et la deuxième pour plus de simplicité.

Je vois plusieurs méthodes :

Méthode n°1:
Pour comparer, il est clair qu'il faut comparer sur des intervalles. Mais, avant cela, tu devrais regarder quel est l'intervalle de chaque fonction à regarder (le domaine de définition). Ensuite, tu pourrais faire un tableau de valeur pour voir quand chaque fonction est croissante, décroissante, égale.
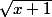
Ensuite, tu peux observer qu'il y a un terme commun aux deux fonctions : (positif et négatif).

Méthode n°2:
Je tiens juste à signaler que cette méthode est pas sûre du tout et n'est pas très mathématique. Si quelqu'un peut corriger ce qui va suivre, ce serait sympathique.
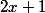
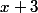
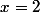
Voici : je pars de l'exemple suivant : comparer et . Dès lors je sais que ces 2 expressions sont (et strictement) suivant . Donc, (où les points sont à compléter par la comparaison). Et du coup, il faut regarder selon la valeur de par rapport à . Si , les membres de l'(in)équation sont égaux, si alors le signe de comparaison entre les membres sera , etc. Mais attentionà l'ordre des 2 membres au départ et à la fin.

Voilà j'espère t'avoir aidé.

[zahira]

vous pouvez donner moi la réponse pour m'assurer de ma réponse et merci

[Lostounet]

vous pouvez donner moi la réponse pour m'assurer de ma réponse et merci

Et c'est quoi ta réponse?

[zahira]

non je voulais dire donnez moi la réponse de votre méthodes s'il vous plait car j'ai arrivée a une fausse réponse

[Lostounet]

non je voulais dire donnez moi la réponse de votre méthodes s'il vous plait car j'ai arrivée a une fausse réponse

Le but du forum est de t'aider à trouver la réponse en t'expliquant. On ne donne pas une réponse toute faite.

[zahira]

ok je vais essayer merci pour la méthode

[zahira]

s'il vous plait comment comparer deux fonction et donner l'ensemble de définition

[Ben314]

Salut,
Pour le domaine de définition, normalement, tu aurais dû voir au collège que existe uniquement lorsque <biiip>
Ensuite, une fois le domaine de définition trouvé, pour résoudre l'inéquation, je pense que le plus simple est d'utiliser le fait que deux réels positifs sont rangés dans le même ordre que leur carré... (et si on est un peu malin, on modifie légèrement l'inégalité de base avant d'élever au carré)

[chan79]

salut
soit la fonction définie par
Si tu peux démontrer avec la dérivée par exemple, que f est décroissante, alors c'est presque fini.
Sinon, la méthode de Ben314 convient bien.

[zygomatique]

salut

j'utilise la notation r(x) pour me simplifier l'écriture ...


comme au collège pour comparer deux nombres on étudie le signe de leur différence ...
on passe à la quantité conjuguée qu'on voyait au collège ... puis en seconde ... puis en première (en particulier quand les sti rencontre les complexes) puis en term pour les S ...




et on réduit au même dénominateur ...

sachant que la fonction racine est croissante et positive la conclusion est immédiate ....

[zahira]

merci pour tout le monde

[chan79]

De rien. Reviens quand tu veux.

[nodgim]

La question peut être "presque trivialement" levée en observant que la dérivée seconde de la fonction racine carrée est négative.