Bonjour,Bonsoir,
Voilà je me retrouve bloque à cette équation où il faut prouver l'égalité,je suis perplexe quant à la méthode à utiliser.. Pourriez vous me venir en aide?
Log{base 3}(Log{base x} 27) = 2
Comment prouver l'égalité de cette équation logarithmique?
8 messages
- Page 1 sur 1
Re: Comment prouver l'égalité de cette équation logarithmiqu
Il faut trouver x ?
Car démontrer une égalité sans connaitre x ça n'a aucun sens...
Car démontrer une égalité sans connaitre x ça n'a aucun sens...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Comment prouver l'égalité de cette équation logarithmiqu
Plutot résoudre l'équation,je me suis mal exprimé
Re: Comment prouver l'égalité de cette équation logarithmiqu
Scorni a écrit:Bonjour,Bonsoir,
Voilà je me retrouve bloque à cette équation où il faut prouver l'égalité,je suis perplexe quant à la méthode à utiliser.. Pourriez vous me venir en aide?
Log{base 3}(Log{base x} 27) = 2
Si tu es à l'aise avec les logarithmes népériens plutôt que les logarithmes de base n, utilise le fait que:
Log(base (x)) (y) = ln(y)/ln(x)
Donc ton équation revient à:
Ln(Ln(27)/ln(x))/ln(3)=2
Où il suffit d'isoler x
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Comment prouver l'égalité de cette équation logarithmiqu
Je n'ai pas trop l'habitude d'utiliser les Ln malheureusement..
Re: Comment prouver l'égalité de cette équation logarithmiqu
Salut,
Perso, dans un cas pareil (avec une base entière), j'utiliserais plutôt la définition du logarithme de base , c'est à dire le fait que
, c'est à dire le fait que 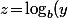\ \Leftrightarrow\ y\!=\!b^z) .
.
Par exemple,\big)\!=\!2\ \Leftrightarrow\ \log_x(27)\!=\!3^2\ \Leftrightarrow\ 27\!=\!\cdots) .
.
Perso, dans un cas pareil (avec une base entière), j'utiliserais plutôt la définition du logarithme de base
Par exemple,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Comment prouver l'égalité de cette équation logarithmiqu
Merci beaucoup Ben,
c'était exactement par cette méthode que je voulais passer mais j'avais des doutes
c'était exactement par cette méthode que je voulais passer mais j'avais des doutes
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
