bonjour,
je n'ai aucune idée de la façon dont je pourrais continuer mon calcul parce que je dois developpé :
rac(S²-4P)
Vous avez une idée ? sa m'aiderais beaucoup :help:
Merci à vous ;) et bonne journée ^^
Comment developpé cette racine?
6 messages
- Page 1 sur 1
bon pour récapituler
S et P sont vus comme la somme et le produit des racines d'un polynome du second degré:
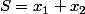
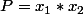
(x-x_2)=x^2-Sx+P)
et effectivement tu retrouves la racine de ton determinant
A ce niveau là tu peux pas vraiment développer plus, il faudrait que tu connaisses les valeurs de tes paramètres.
Sinon tu peux dire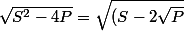(S+2\sqrt{P})}) mais c'est pas forcément utile.
mais c'est pas forcément utile.
S et P sont vus comme la somme et le produit des racines d'un polynome du second degré:
et effectivement tu retrouves la racine de ton determinant
A ce niveau là tu peux pas vraiment développer plus, il faudrait que tu connaisses les valeurs de tes paramètres.
Sinon tu peux dire
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 108 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
