Combinatoire
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 16:18
par globule rouge » 02 Juin 2012, 16:18
Bonjour

Je cherche à calculer
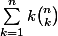
.
J'arrive à
\sqrt{2}^{n+1})
mais j'ai dû supposer que n est impair :/ Et je ne suis même pas sûre que c'est juste !
Quelqu'un a-t-il une idée pour m'aider à trouver la réponse ?
Merci !
Julie

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Juin 2012, 17:21
par chan79 » 02 Juin 2012, 17:21
globule rouge a écrit:Bonjour

Je cherche à calculer
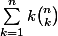
.
J'arrive à
\sqrt{2}^{n+1})
mais j'ai dû supposer que n est impair :/ Et je ne suis même pas sûre que c'est juste !
Quelqu'un a-t-il une idée pour m'aider à trouver la réponse ?
Merci !
Julie
Bonjour Julie
Essaie avec
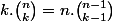
.
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
 par gdlrdc » 02 Juin 2012, 17:22
par gdlrdc » 02 Juin 2012, 17:22
C'est une somme de nombres entiers donc je vois pas ce que viens faire rac(2) dans ta formule?
1) Je te conseille d'utiliser la formule du binôme de newton
(1+x)^n=somme des x^k* C(n,k)
puis tu dérives dans chaque membre et tu prends la valeur pour x=1, et tu devrais pas être loin de la solution
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 17:26
par globule rouge » 02 Juin 2012, 17:26
Merci beaucoup Chan79 :)
En ce qui concerne la racine de 2, je sais que le résultat n'est pas bon mais il est plausible ^^ car j'ai supposé que n+1 est divisible par 2

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Juin 2012, 17:48
par chan79 » 02 Juin 2012, 17:48
gdlrdc a écrit:C'est une somme de nombres entiers donc je vois pas ce que viens faire rac(2) dans ta formule?
Les apparences sont parfois trompeuses, le nombre suivant est entier quel que soit l'entier naturel n
^n-\(\fra{1-\sqrt{5}}{2}\)^n\))
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 02 Juin 2012, 17:56
par vincentroumezy » 02 Juin 2012, 17:56

ne sera jamais entier,si ?
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 18:01
par globule rouge » 02 Juin 2012, 18:01
vincentroumezy a écrit:
ne sera jamais entier,si ?
si n est impair et supérieur à 1, si

-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 02 Juin 2012, 18:02
par manoa » 02 Juin 2012, 18:02
vincentroumezy a écrit:
ne sera jamais entier,si ?
euh pour n impair si !
sinon je pense que la méthode proposé par gdlrcd est sympa .
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 02 Juin 2012, 22:39
par Iroh » 02 Juin 2012, 22:39
!(n-k)!}\\<br /> &=& \sum_{k=1}^n n \frac{(n-1)!}{(k-1)!(n-k)!}\\<br /> &=& \sum_{k=1}^n n \binom{n-1}{k-1}\\<br /> &=& n \sum_{k=1}^n \binom{n-1}{k-1}\\<br /> \end{eqnarray})
On pose
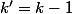
:
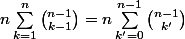
On pose
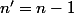
:
\sum_{k'=0}^{n'} \binom{n'}{k'}\\<br /> &=& (n'+1)2^{n'}<br /> \end{eqnarray})
d'où, comme
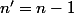
:
2^{n'} = n 2^{n-1})
Sauf erreur.
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 22:43
par globule rouge » 02 Juin 2012, 22:43
Non, c'est bien ça :)
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 03 Juin 2012, 08:42
par vincentroumezy » 03 Juin 2012, 08:42
chan79 a écrit: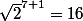
Je suis vraiment pas assez concentré, quand on voit que
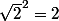
:mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités