Colinéarite 2nde

par **Billball** » 31 Oct 2006, 16:42

Bijour,

Quelqu'un pourrait-il m'expliquer clairement en montrant un exemple comment procéder pour montrer que 2 vecteurs sont colinéaires, j'y arrive mais des qu'il y a des facteurs devant un ou plusieurs vecteurs j'y arrive pas :cry:

par **matteo182** » 31 Oct 2006, 17:49

Salut,

et

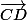
sont colinéaires s'il existe un réek tel que :

.
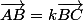
Exemple :
Soit

de coordonnées (1;2) et soit

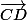
de coordonnées (4;8).
On remarque que :

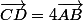
Donc

et

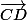
sont colinéaires.

par **Billball** » 31 Oct 2006, 18:10

Heuuu, j'arrive à m'repérer quand il y a un repère mais là dans mon exo, c'juste : 3vect.AC + vect.CB - 2vect.BD = vect. 0
D'abord j'passe le vect. CB à la place du nul, c'qui donne vect. BC et ensuite :cry:

par **matteo182** » 31 Oct 2006, 18:17

C'est quoi la question aussi ?

par **Billball** » 31 Oct 2006, 18:23

Ah ups -_-", la question bah faut démontrer que vect. AB et vect. CD sont colinéaires ;)

par **matteo182** » 31 Oct 2006, 18:28

Utilises Chasles en introduisant le point B dans le vecteur AC, et le point C dans le vecteur BD.
Ca devrait marcher. Le but c'est quil nous reste simplement des vecteur AB et CD et doinc de faire sauter les vecteurs BC.
Fait ça et ca devrait marcher à vu d'oeil.

par **Billball** » 31 Oct 2006, 18:31

Ok mais j'comprends pas j'en fais kwa des facteurs... j'met : 3 (vect.AB + vect. BC)? Désolé j'ai vraiment du mal :triste:

par **matteo182** » 31 Oct 2006, 18:33

Oué ! et fait pareil en introduisant le point C dans le vecteur BD. Ensuite tu développes et normalement la magie se produit.

par **Billball** » 31 Oct 2006, 18:45

Bué, hum corrige mouwa si c'est faux :

3 vect.AC + vect.CB - 2 vect.BD = vect.0
3(vect.AB + vect.BC) - 2(vect. BC + vect. CD) = vect. BC
3vect.AB + 3vect.BC - 2vect.BC + 2vect.CD = vect. BC
3vect.AB + vect.BC + 2vect.CD = vect.BC
3vect.AB + 2vect.CD = vect.0
3vect.AB=2vect.DC
vect.AB=2/3vect.DC

par **matteo182** » 31 Oct 2006, 18:53

3(vect.AB + vect.BC) - 2(vect. BC + vect. CD) = vect. BC
3vect.AB + 3vect.BC - 2vect.BC + 2vect.CD = vect. BC

Dans la 2eme ligne , c'est -2 vect CD

Donc à la fin ca nous donne :

vect AB = 2/3 vect CD

Voilà.

par **Billball** » 31 Oct 2006, 18:57

Oui pas fais attention, c'était - ^^, m'enfin grâce à touwa, j'ai compris l'principe, j'te remercie IN-FI-NI-MENT ^_^"

:we:

Colinéarite 2nde

Colinéarite 2nde

Qui est en ligne