Coefficients binomiaux

[GeorgeB]

Bonjour , j'ai des problèmes avec les coefficients binomiaux, je dois montrer plusieurs formules,

Je connais les deux basiques, celle de la somme des combinaisons et celle avec le (-1)^k devant.

1) Trouver

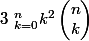
2) Calculer
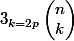
(k pair)
3) Calculer
pour p donné.

4) Calculer
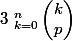
pour p donné aussi.

5) Calculer pour p donné
Je vous remercie !!

[Sa Majesté]

Salut

Tu as globalement 2 possibilités pour résoudre ces problèmes :
- tu conjectures la réponse à l'aide de quelques cas et tu démontres ta conjecture par récurrence
- tu démontres directement en triturant les factorielles

La 1ère possibilité n'est pas la plus simple car la conjecture est souvent difficile à faire

Par ex











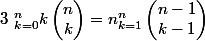
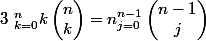
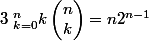
Avec cette méthode il faut faire attention aux premiers coefficients 0,1 et aux derniers n-1, n car les changements d'indices peuvent générer quelques soucis

[GeorgeB]

salut ! Merci.

Par contre ça risque d'être dificile sur certains. MAis on m'a dit que il fallait directement utiliser le binôme pour résoudre ce genre d'exos. Comment faire ?

Merci :we:

[benekire2]

bah pour la première .. tu peut prendre (1+x)^n et dériver deux fois, ce qui donne n(n+1)(1+x)^(n-2) et du coup comme

Du coup, en écrivant que k²=k(k-1)+k tu t'en sort. Il y a surement mieux ...

Ensuite pour la 2 : Tu sais que Somme des pairs = Somme des impairs et que Somme paire + Somme impairs=2^n --> tu peut conclure que ça fait 2^(n-1)

Pour la 3, faut identifier avec (1+x)^(n+p)

[Sa Majesté]

Si tu as le droit de dériver alors oui c'est une bonne méthode

[benekire2]

pourquoi il pourrait pas dériver ?

[GeorgeB]

Ok merci, je vous tient au courrant des mes avancé.