Cherche exo dérivées 1ère S

[mathelot]

Bonjour,


je cherche des énoncés d'exercices (intéressants) sur les nombres dérivés, fonctions dérivées et leurs applications, niveau 1ère S.

si vous avez des idées d'exos, mêmes informelles, je rédigerai.


le souçi, c'est de bien doser la difficulté, j'ai vû un exo intéressant
sur la primitive impaire de
mais déja en TS, c'était limite trop difficile...


Cx,

[mathelot]

re,
je viens d'en bricoler trois:

exo 1:
soit dérivable sur . En utilisant la définition:


montrer que si f est paire, est impaire
et si f est impaire, est paire.

exo2:
soit
et a<b.

vérifier qu'il existe tel que


exo3
soit
a) trouver la dérivée f '
b) écrire l'équation de la tangente T à la courbe de f en x=1
c) en étudiant les variations de

montrer que la courbe de reste sous la droite T.

exo4:
soit
étudier les variations de f sur
En déduire que f admet un minimum global sur cet intervalle.


c bon ? d'autres idées ?

[Huppasacee]

Bonjour

choisir un polynôme du troisième degré, représenté par la courbe C

et un paramètre m

pour quelles valeurs de m existe-t-il un ou des tangentes à C parallèles à la droite
y = mx - 3 ( par exemple )

[mathelot]

re,

est-ce que vous pourriez me tester cet exercice (original) ?
.........

[Huppasacee]

As tu essayé avec un polybôme quelconque ?

En fait, cela se termine par un calcul de déterminant d'un trinôme du second degré.


Un autre exercice et de trouver l'équation d'une parabole en donnant 3 indications

La plus classique est de donner 3 points

Sinon 1 point avec ses coordonnées ( x1 ; f(x1) )
+ la pente de la tangente en ce point ou en un autre point ( x2 + f ' (x2) )
+ une troisième condition, par exemple la tangente au point d'abscisse x3 passe par le point ( xo, yo)

[mathelot]

merçi bcp, Huppasacee,

en vlà un que j'ai redécouvert et réécrit:

exo 5:
Soit P le plan muni d'un repère orthonormé (O,I,J)
C la parabole d'équation
A le point de coordonnées (2,2)
M un point quelconque de la courbe C d'abscisse

calculer
En étudiant les variations de
montrer que h admet un minimum global pour une valeur .
On note le point de la courbe C d'abscisse .

Montrer que les droites et la tangente à la courbe C en sont perpendiculaires.

[mathelot]

re,


en voila un autre, je ne sais s'il est faisable...

exo 6

soit P le plan orienté muni d'un repère orthonormé (O,I,J)

soit C la parabole d'équation

Trouver le lieu des points M du plan
où l'on peut mener deux tangentes à C
faisant entre elles un angle de

si c'est simple, je le réécrirai avec un polynôme de degré 3.

[Huppasacee]

re,


en voila un autre, je ne sais s'il est faisable...

exo 6

soit P le plan orienté muni d'un repère orthonormé (O,I,J)

soit C la parabole d'équation

Trouver le lieu des points M du plan
où l'on peut mener deux tangentes à C
faisant entre elles un angle de

si c'est simple, je le réécrirai avec un polynôme de degré 3.

L'exercice est faisable, mais donne lieu à des calculs assez longs pour la 1ère S , me semble-t-il

[mathelot]

re,


en voila un autre, je ne sais s'il est faisable...

exo 6

soit P le plan orienté muni d'un repère orthonormé (O,I,J)

soit C la parabole d'équation

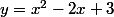
Trouver le lieu des points M du plan
où l'on peut mener deux tangentes à C
faisant entre elles un angle de

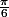
si c'est simple, je le réécrirai avec un polynôme de degré 3.

j'ai commencé à le résoudre, les calculs sont longs et compliqués:

on écrit le système vérifié par les coordonnées du point de rencontre des tangentes



et le produit scalaire des vecteurs directeurs des deux tangentes:


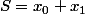
l'idéée géniaaale, c'est de calculer X et Y en fonction de et



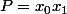
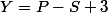
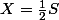
soit



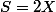
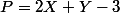
et on reporte S et P en fonction de X et Y dans le produit scalaire...

évidemment, si on considère qu'on mène à la courbe deux tangentes
perpendiculaires, le produit scalaire nul donne:


et on obtient plus facilement le lieu des points.
Je vais réécrire l'exo 6 en 6bis.

[mathelot]

re,

exo 6bis (exo 6 simplifié)

Soit P le plan muni d'un repère orthonormé (O,I,J).
Soit C la courbe d'équation
et deux points distincts de C d'abscisses et
et les droites tangentes à C en et

a) On pose et P=
Soit le point d'intersection des tangentes et
démontrer que et

on suppose que et sont perpendiculaires.

b) Montrer que
c) En déduire le lieu des points du plan d'où l'on peut tracer
deux tangentes perpendiculaires à C.

ça parait bizarroïde comme résultat ? quelqu'un peut faire mon exo 6 bis ?
On trouve bien pour une droite horizontale ?

merçi d'avance.

[Huppasacee]

Pour confirmer ou infirmer :


Ma démarche a été autre

Prenons M ( X ; Y)

les droites Da passant par M auront pour équation générale
y = ax + (Y - aX)

cherchons les points d'intersection de Da avec C

donc résoudre :

1/2 x² - x = ax + (Y - aX)

x² -2x - 2ax -2(Y-aX) = 0

x² -2x(1+a) - 2(Y-aX) =0


Pour que Da soit tangente , l'équation doit avoir une seule solution

donc discriminant nul .


(1+a)² + 2(Y-aX) = 0


Si 2 solutions a1 et a2


on a

a1*a2 = ...

a2 - a1 = ...

et , pour mémoire ( ne servira pas ) a1 + a2 = ....



les 2 tangentes Ta1 et Ta2 issues de M auront pour coeff directeurs a1 et a2 , qui devront vérifier :

angle ( Ta1, Ta2) = pi/6

donc tan (pi/6) = ( a2 - a1)/ ( 1 + a1*a2)

on en tire une équation du lieu de points M vérifiant la condition citée
qui me semble différente de ta proposition , mais il est possible que j'aie fait une ou des erreurs de calcul

A revoir plus en détail

[busard_des_roseaux]

bonsoir,


Avec un angle
l'équation aux coefficients directeurs donne



On trouve que le lieu des points du plan d'où l'on peut mener deux tangentes perpendiculaires à C est la droite horizontale d'équation Y= -1.



une droite tangente en à une courbe, représentative d'une fonction f, est définie comme une droite de pente et non pas comme une sécante à point double, ce qui n'impose même pas
que f soit dérivable...

Est-ce évident de faire le lien entre les deux définitions ?

[Huppasacee]

L'angle pi/2 entre les tangentes serait- il un cas particulier donnant un droite horizontale comme lieu de points ?

quant à f'(xo) , il est défini comme étant la limite de ?. Ne serait ce pas la limite du coefficient directeur d'une sécante ? Quelle en est la conséquence graphique ?