Cherche un astuce pour linéariser n'importe quelle fonction

[SeifMaths]

Bonjour,
J'ai passé mon devoir aujourd'hui et j'ai rencontré cette question:
Linéariser Sin(3x)Cos²(x).

J'ai procédé en faisant Cos²(x) = 1 - Sin²(x)
or
1 - 2sin²(x) = cos (2x) donc sin²(x) = (1 - cos(2x))/2
D'où Sin(3x)Cos²(x) = Sin(3x) - Sin(3x)/2 - Sin(3x)Cos(2x)/2
Et je me suis arrêté à ce niveau car ça devient de plus en plus compliqué.. Avez-vous un astuce pour linéariser de telles fonctions sans perdre du temps? Et biensur comment linéariser celle-là?

[Carpate]

Par exemple en utilisant :

et

[SeifMaths]

Par exemple en utilisant :

et

J'aime bien cette méthode, toutefois il n'y a pas une autre méthode "passe partout"?

[Carpate]

Utiliser l'exponentielle complexe 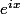mais c'est balourd ...

[SeifMaths]

Utiliser l'exponentielle complexe mais c'est balourd ...

Ah oui je préfère ne rien faire au lieu de perdre 10 minutes en vérifiant les puissances et les e.
Donc il me semble que je dois m'exercer plus sur la linéarisation afin d'éviter ce genre de problèmes, merci beaucoup!

[chan79]

Bonjour,
J'ai passé mon devoir aujourd'hui et j'ai rencontré cette question:
Linéariser Sin(3x)Cos²(x).

J'ai procédé en faisant Cos²(x) = 1 - Sin²(x)
or
1 - 2sin²(x) = cos (2x) donc sin²(x) = (1 - cos(2x))/2
D'où Sin(3x)Cos²(x) = Sin(3x) - Sin(3x)/2 - Sin(3x)Cos(2x)/2

salut
sin(3x)(1-sin²(x))=sin(3x)-sin(3x)(1-cos(2x))/2
=sin(3x)/2+(sin(3x)*cos(2x))/2
sin a cos b=(sin(a+b)+sin(a-b))/2
donc
sin(3x)/2+sin(5x)/4+sin(x)/4