La chasse aux angles

[Timothé Lefebvre]

Dors un peu quand même, ce serait con de t'effondrer sur ta copie !

[Olympus]

Dors un peu quand même, ce serait con de t'effondrer sur ta copie !

Ce serait aussi con de me faire éliminer juste parce que je n'ai pas pris le temps de réviser la géométrie ( 2 des 4 exos des olympiades sont sur la géométrie, et y a un seul exo sur les inégalités ) :marteau:

Enfin, vaut mieux m'effondrer sur ma copie comme ça j'aurais une excuse :id:

Bon allez, merci à tous pour votre aide !

[Timothé Lefebvre]

De rien ;)

On attend ton sujet demain soir au fait, bien entendu :D

[benekire2]

Non, ce n'est pas demain que sont ses olympiades mais après demain, mais il ne pourra pas bosser demain apparemment ... C'est ce qu'il m'a confirmé sur un autre Topic :) ; Mais ce sont les Olympiades Nationales, donc ça devrait être plus facile ( enfin différent !!) des exos d'OIM.

[Timothé Lefebvre]

Tiens d'ailleurs moi j'ai un exo d'OIM en cours qui me bloque sur la démo :lol: Je vous poste ça ;)

[benekire2]

Vas y toujours :lol:
Aufait tu aurais une petite correction des deux exos de la dernière fois ( si t'en as pas, te casse pas ...) ?
Muchas gracias !

[Timothé Lefebvre]

Oui j'en ai une, malheureusement je suis over-booké ce soir (toujours ce DS de Bio ...). Je te mets ça sur le fofo demain midi, promis !

[Olympus]

Bon bon, comme je l'avais dit, j'ai foiré l'exo de géométrie, sinon ça va, je n'ai pas affiché de pitié aux exos d'inégalités

Ah oui, et le truc le plus fun, c'est que j'ai passé PAR ERREUR les olympiades de la classe Terminale S ...., mais ça va, eux ils ont deux exercices d'inégalités sur 4 ce qui m'était favorable ( vu que j'ai très bien travaillé les inégalité avant ), et les Première S avec lesquelles je devais passer les olympiades avaient seulement un exercice d'inégalités et quelques exos d'arithmétique, donc j'ai choisi de continuer de passer avec la Terminale S et ils n'ont vu aucun problème

Donc voilà, y avait 4 exos : 2 sur les inégalités, 1 en géométrie, et un autre sur les systèmes .

J'ai fini les 2 sur les inégalités en 15~20 minutes, puis les 2h40~2h45 restantes je testais tout et n'importe quoi pour répondre aux autres exos mais je n'ai pas réussi donc je n'ai répondu qu'à deux exos sur 4 ( mais j'en suis fier quand même vu que je n'ai révisé que les inégalités ) .

Voici nos olympiades ( enfin celles des Terminales S lol ) :

Exercice 1:

Soient , et trois réels positifs tels que 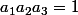( donc il est évident qu'ils sont strictement positifs ^^ ) .

Montrer que :



Ma solution :

Tout d'abord, on sait que ( que j'ai prouvé sur ma feuille pour être sûr ) .

Donc :





En sommant, on obtient :







On sait que ( proprio que j'ai aussi démontré sur la feuille au cas où ), donc :



Et enfin :

[Olympus]

euh je ne sais pas ce qui ne va pas avec mon code latex ...

[Timothé Lefebvre]

Je t'ai envoyé la modif'.

[Olympus]

D'accord, merci !

Voilà c'est bon pour le premier exo, je posterai le reste demain car maintenant j'ai plus de temps ^^

[Timothé Lefebvre]

Bon ça va, à première vue c'était pas trop dur ;)
J'espère que tu t'en es sorti !

[Olympus]

Bon ça va, à première vue c'était pas trop dur
J'espère que tu t'en es sorti !

Euh quand même, vu qu'il n'y a pas d'entrainement des équipes chez nous ( pas comme chez vous en France je crois ), la plupart des élèves ne connaissaient pas les techniques ( pourtant faciles ) du et vu qu'ils n'ont jamais eu l'occasion de les appliquer . Les profs aussi ne nous ont pas aidé à nous préparer donc voilà c'était chacun pour soi et je suis tout à fait sûr que seuls trois élèves sur tout le lycée ont fait les deux exos d'inégalité 100% corrects ( moi, le mec anormal qui arrive à avoir tout perfect aux olympiades, et un autre copain ) .

Donc même si je n'ai eu que la moyenne ( 2 exos, sur les inégalités bien sûr, sur 4 réalisés, ah oui, j'ai aussi dessiné la figure du 4ème éxo loool :ptdr: ), j'en suis quand même fier vu que je n'ai révisé rien d'autre que les inégalités, donc si j'avais pris le temps de réviser aussi la géométrie, j'aurais eu 3 exos sur 4 :we:

Sinon, vi je suis sûr de me faire qualifier pour les prochaines olympiades, mais là je préparerait tout et pas seulement les inégalités !! ( chaque weekend je bosserait comme un nolife )

[benekire2]

Oh ca va celui la il roule pépère comme exo ... Après j'ai pas vu les autres.
N'ayant pas travaillé sur les inégalités, je le trouve assey abordable ce premier exo .

[Olympus]

Exercice 2 :

Soien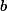t , et les longueurs des côtés d'un triangle tel que .

Montrer que est la longueur du plus petit côté de ce triangle .

( ps : la plupart ont fait n'importe quoi sur cet exercice, donc j'ai un avantage sur le classement vu que je fais partie des trois qui l'ont fait sans fautes ^^ )

Ma solution :

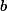et et sont les longueurs des côtés d'un triangle, donc :

et ( bien sûr il y a aussi une troisième inégalité, mais pour l'instant je n'ai besoin que des deux )

Donc



On sait que :

Donc :




De la même façon, on trouve aussi

Donc est la longueur du plus petit côté de ce triangle .

[benekire2]

Oui, c'est vrai que c'est chacun pour sois, et je t'assure qu'il n'y a pas un élève sur 1000 au niveau global, qui sait résoudre des exercices d'inégalités, tout simplement parce que les méthodes pour résoudre ce type d'exos n'est pas enseigné au lycée.

[benekire2]

une question , tu n'as révisé les inégalités qu'avec Animath ? Ou bien tu as lu inequalities ? Ou d'autres sites? ?

Merci olympus.

[Olympus]

une question , tu n'as révisé les inégalités qu'avec Animath ? Ou bien tu as lu inequalities ? Ou d'autres sites? ?

Merci olympus.

Que Animath pour l'instant, j'ai pas encore abordé les deux livres "The Cauchy-Schwarz Master Class" et "Geometry Revisited" ( je ferais ça pendant les vacs ) .

[benekire2]

OK :) Merci bien olympus ^^

[Olympus]

Je continue, l'exo de géométrie :

Exercice 3 :

Deux cercles et se coupent en et . La tangente au cercle passant par coupe le cercle en un point , et la tangente au cercle passant par coupe le cercle en un point . La demi-droite passant par ( intérieure à l'angle ) coupe respectivement les cercles , et le cercle circonscrit au triangle en , et .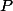

Montrer que .

Ma solution :

Euh rien :ptdr: