Chapitre dérivation, term
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
henriettedumans
- Membre Naturel
- Messages: 58
- Enregistré le: 27 Fév 2013, 16:51
-
 par henriettedumans » 08 Aoû 2013, 05:19
par henriettedumans » 08 Aoû 2013, 05:19
Bonjour à tous.
Au petit-déj´ ce matin une petite dérivation.
Chercher la limite de la fonction au point donné:
f(x)=(1-cos(2x))\x^2 En 0
Je ne fais que tomber sur des f.i. Je ne sais que faire du x^2. J ai tenté un changement de variable mais sans succès......
-
Boss_maths
- Membre Naturel
- Messages: 82
- Enregistré le: 11 Déc 2010, 08:24
-
 par Boss_maths » 08 Aoû 2013, 07:04
par Boss_maths » 08 Aoû 2013, 07:04
Bonjour,
Ok, c'est :

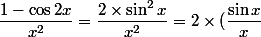^2)
En tenant compte de :
=1)
...
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 08 Aoû 2013, 07:55
par jlb » 08 Aoû 2013, 07:55
Salut, tu peux aussi utiliser un petit développement limité cos(2x)=1 - 4x²/2 +o(x) d'où une limite valant 2
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Aoû 2013, 09:16
par vincentroumezy » 08 Aoû 2013, 09:16
Les DL sont hors programme en terminale :lol3:
-
henriettedumans
- Membre Naturel
- Messages: 58
- Enregistré le: 27 Fév 2013, 16:51
-
 par henriettedumans » 08 Aoû 2013, 12:49
par henriettedumans » 08 Aoû 2013, 12:49
Boss_maths a écrit:Bonjour,
Ok, c'est :

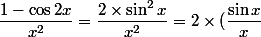^2)
En tenant compte de :
=1)
...
Eurêka!!!! :we:
-
henriettedumans
- Membre Naturel
- Messages: 58
- Enregistré le: 27 Fév 2013, 16:51
-
 par henriettedumans » 08 Aoû 2013, 12:50
par henriettedumans » 08 Aoû 2013, 12:50
jlb a écrit:Salut, tu peux aussi utiliser un petit développement limité cos(2x)=1 - 4x²/2 +o(x) d'où une limite valant 2
Je comprendrais certainement cette phrase d'ici quelques temps!!!!! :hein: :we:
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Aoû 2013, 12:55
par vincentroumezy » 08 Aoû 2013, 12:55
Ca veut juste dire que autour de 0, cos(2x) c'est à peu près pareil que 1-2x²
Précisément, cos(2x)=(au sens d'une égalité réelle, ie, c'est VRAIMENT la même chose)1-2x²+un terme qui est négligeable devant x² au voisinage de 0.
-
majta
- Messages: 1
- Enregistré le: 09 Jan 2013, 18:56
-
 par majta » 18 Aoû 2013, 09:09
par majta » 18 Aoû 2013, 09:09
Ca devrait intéresser du monde ici ! Le micro-soutien en maths :
http://hop-maths.frNon ? :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
