Changer une expression
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 22 Avr 2013, 14:26
par mella12 » 22 Avr 2013, 14:26
Bonjour à tous, je bloque sur une petite question que voici :
Montrer que pour tout réel x,
=ln(e^x+1)-\frac{2}{3}x)
sachant que
=ln(1+e^{-x})+\frac{1}{3}x)
J'ai déjà eu quelques conseils mais je suis toujours bloqué, on m'a notamment conseillé de factoriser par

et d'utiliser
=ln a + ln b)
J'ai fais :
=ln(1+e^{-x})+\frac{1}{3}x)
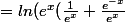)+\frac{1}{3}x)
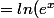 + ln(\frac{1}{e^x}+e^{-2x})+\frac{1}{3}x)
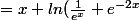+\frac{1}{3}x)
Et après je ne sais pas quoi faire, pouvez vous m'aider ou me corriger svp, merci.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 22 Avr 2013, 14:31
par chan79 » 22 Avr 2013, 14:31
salut
=ln(1+e^{-x})+\fra{x}{3})
=
=ln(1+\fra{1}{e^{x}})+\fra{x}{3})
=
=ln(\fra{e^x +1}{e^{x}})+\fra{x}{3})
=
ensuite ln(a/b)=ln(a)-ln(b)
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 22 Avr 2013, 14:38
par mella12 » 22 Avr 2013, 14:38
chan79 a écrit:salut
=ln(1+e^{-x})+\fra{x}{3})
=
=ln(1+\fra{1}{e^{x}})+\fra{x}{3})
=
=ln(\fra{e^x +1}{e^{x}})+\fra{x}{3})
=
ensuite ln(a/b)=ln(a)-ln(b)
+\fra{x}{3})
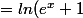-ln(e^x)+\frac{x}{3})
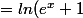-x+\frac{x}{3})
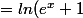-\frac{2}{3}x)
Ca paraissait tellement dur alors qu'en réalité pas du tout.. Merci beaucoup !! :we:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 22 Avr 2013, 14:42
par chan79 » 22 Avr 2013, 14:42
mella12 a écrit:
Ca paraissait tellement dur alors qu'en réalité pas du tout.. Merci beaucoup !! :we:
c'est souvent comme ça ... bonne raison pour toujours persévérer ... :zen:
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 22 Avr 2013, 15:03
par mella12 » 22 Avr 2013, 15:03
Oui mais à trop réfléchir et pas réussir ça devient agaçant lol. D'ailleurs j'ai une autre question, je dois calculer la dérivée, j'ai trouvé

Et je dois retrouver la dérivée de l'énoncé qui est
})
Cependant je n'arrive pas à la retrouver en mettant au même dénominateur, pouvez vous m'aider svp ? La dérivée que j'ai trouvée est-elle juste ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 22 Avr 2013, 15:11
par chan79 » 22 Avr 2013, 15:11
mella12 a écrit: La dérivée que j'ai trouvée est-elle juste ?
oui, et en réduisant au même dénominateur, tu tombes directement sur ce qui est demandé. Mets ton calcul
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 22 Avr 2013, 15:24
par mella12 » 22 Avr 2013, 15:24
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités