Changement d'inconnue dans une équation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 17:30
par boubounchk » 11 Fév 2007, 17:30
Bonjour pouvez-vous m'aider pour un exercice sur lequel je bloque depuis 2 jours.
On me donne l'équation (E) x^4+x²-2=0.
Si l'on remplace x² par X, par quoi dois-je remplacer x^4?
Je dois résoudre la nouvelle équation (E'), donner les solutions et en déduire les solutions de (E).
J'ai trouvé que (E') est x²+x-2=0.
Les deux solutions sont 2 et -1.
Mais quelles sont les solutions de (E)?
Merci d'avance.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 11 Fév 2007, 17:34
par Monsieur23 » 11 Fév 2007, 17:34
x^4+x²-2=0.
Ceci est pareil que d'écrire
^2 + x^2 -2 = 0)
Voilà =)
« Je ne suis pas un numéro, je suis un homme libre ! »
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 17:49
par boubounchk » 11 Fév 2007, 17:49
Merci pour votre aide mais cela ne me donne pas une équation du second degré que je puisse résoudre...
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 11 Fév 2007, 17:55
par allomomo » 11 Fév 2007, 17:55
salut
 : x^4+x^2-2 = 0)
On pose
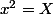
Ainsi on a :
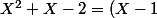(X+2)=0)
On a alors :
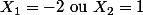
Or :
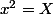
D'où :
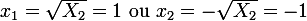
(E) possède deux solutions réelles : -1 et 1
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 18:04
par boubounchk » 11 Fév 2007, 18:04
Merci beaucoup!!
Mais quelqu'un m'a dit que pour résoudre x^4+x²-2=0, on doit changer l'inconnue et que cela donne:
x²+x-2=0
Après je résouds et je trouve 1 et -2.
Qu'elle est mon erreur?
Merci d'avance.
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 18:07
par boubounchk » 11 Fév 2007, 18:07
Ce que je ne comprend pas c'est comment vous faites pour trouver -1 et 1 comme solutions?
Merci d'avance.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Fév 2007, 18:07
par Clembou » 11 Fév 2007, 18:07
boubounchk a écrit:Merci beaucoup!!
Mais quelqu'un m'a dit que pour résoudre x^4+x²-2=0, on doit changer l'inconnue et que cela donne:
x²+x-2=0
Après je résouds et je trouve 1 et -2.
Qu'elle est mon erreur?
Merci d'avance.
Regarde plus en haut :we: Là c toujours la même inconnue donc si on note (E)
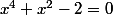
et (E')
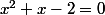
, (E) et (E') n'ont pas le même nombre de solutions (cela dépend dans quels ensembles on se place). Quand tu changes de variables essaie de les différencier c'est-à-dire tu changes la lettre (voir plus haut).
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Fév 2007, 18:09
par Clembou » 11 Fév 2007, 18:09
boubounchk a écrit:Ce que je ne comprend pas c'est comment vous faites pour trouver -1 et 1 comme solutions?
Merci d'avance.
Quand tu poses
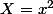
, l'équation se transforme en

, là il y a deux solutions donc -2 et 1 mais ce qu'on veut ce sont les solutions en fonction de x. Donc comme
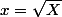
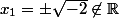
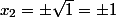
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 18:10
par boubounchk » 11 Fév 2007, 18:10
Merci Clembou!
J'ai trouvé -2 et 1 comme solutions pour (E'), mais je ne comprend pas comment on trouve les solutions de (E)?
Merci pour votre aide.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Fév 2007, 18:14
par Clembou » 11 Fév 2007, 18:14
boubounchk a écrit:Merci Clembou!
J'ai trouvé -2 et 1 comme solutions pour (E'), mais je ne comprend pas comment on trouve les solutions de (E)?
Merci pour votre aide.
Regarde plus haut

-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 18:21
par boubounchk » 11 Fév 2007, 18:21
Merci! J'ai un autre exo dans le même style
(E):-2x^4+3x²-1=0
Donc (E'): -2x²+3x-1=0 ?
Merci de me répondre si vous le pouvez.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Fév 2007, 18:24
par Clembou » 11 Fév 2007, 18:24
boubounchk a écrit:Merci! J'ai un autre exo dans le même style
(E):-2x^4+3x²-1=0
Donc (E'): -2x²+3x-1=0 ?
Merci de me répondre si vous le pouvez.
:--: Appliques ce que je t'ai dit plus en haut (n'oublie pas de changer la lettre de la variable quand tu fais un changement de variable, sinon tu vas tout t'embrouiller) :++:
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 18:30
par boubounchk » 11 Fév 2007, 18:30
???????????
SVP!!!!! :briques:
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Fév 2007, 18:36
par Clembou » 11 Fév 2007, 18:36
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 18:45
par boubounchk » 11 Fév 2007, 18:45
Merci, je sais résoudre mais je n'arrive pas à transformer (E) en (E')!
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Fév 2007, 18:47
par Clembou » 11 Fév 2007, 18:47
boubounchk a écrit:Merci, je sais résoudre mais je n'arrive pas à transformer (E) en (E')!
Ah ! Bien tu dis que (E)
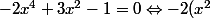^2+3(x^2)-1)
d'où tu poses
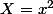
pour t'amener à une équation de second degré.
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 18:58
par boubounchk » 11 Fév 2007, 18:58
Merci beaucoup!
Donc je récapitule:
J'obtiens -2x²+3x-1=0
2 solutions: 1/2 et 1
les solutions de X
racine de 1/2
racine de -1/2
racine de 1
racine de -1
Mais la racine d'un nombre négatif n'existe pas?
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 11 Fév 2007, 19:05
par boubounchk » 11 Fév 2007, 19:05
Un autre exemple:
(E) :x^4+5x²+4=0
(E'): x²+5x+4=0
Alors: 5²-4(1x4)
=25-16
=9
Donc 2 solutions:
x1=-1
x2=-4
Les solutions de X:
???? vu que les racines négatives n'existent pas!!
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 11 Fév 2007, 20:59
par allomomo » 11 Fév 2007, 20:59
Re -
Aucune solution réelle puisque le delta de ton (E') est négatif
-
boubounchk
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Fév 2007, 17:21
-
 par boubounchk » 12 Fév 2007, 15:06
par boubounchk » 12 Fév 2007, 15:06
Mais non delta est positif et égal à 9!!
Il y a donc bien 2 solutions!!!!!!!!!!!!!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
