Cercles/Trigono

par **Noval** » 13 Juil 2007, 22:29

C'est un vrai casse-tête ce truc-là.

par **prody-G** » 13 Juil 2007, 22:32

ouaip m'y pencherai demain...a+tard

par **Noval** » 13 Juil 2007, 22:33

À plus tard.

par **emdro** » 14 Juil 2007, 10:26

Noval,

Premier exo
Si R est le rayon et t l'angle au centre (en radians), l'arc mesure Rt.
Le périmètre nous fournit 2R+Rt=20 soit R(2+t)=20.
La surface est S=tR²/2 (proportionnalité).

Tu as donc

Tu dérives la fonction de t obtenue, et tu n'es pas loin de trouver t=2 radians,
et donc R=5cm.

Deuxième exo

C'est moins drôle.

2R+AB=4
AB*h/2=1, h étant la hauteur issue de O dans OAB.

D'après le théorème de Pythagore, h²+AB²/4=R²

Notons a=AB/2 pour y voir plus clair.

R+a=2
ah=1
h²+a²=R²

Trois équations, trois inconnues, on va s'en sortir.
a=2-R
h²=1/a²

d'où

Si tu arranges un peu, tu tombes sur

Malheureusement, on ne peut pas exprimer la solution de cette équation. On est réduit à l'approximation numérique: R vaut environ 2.4196.
Ce qui est impossible car le périmètre vaudrait nécéssairement plus de 4.

Le triangle sur lequel on a travaillé n'existe donc pas!

par **emdro** » 14 Juil 2007, 10:57

Tu peux te convaincre du résultat précédent en étudiant l'aire et le périmètre d'un secteur circulaire de rayon R et d'angle au centre t.
Son périmètre est

.
Son aire est

Si tu étudies le rapport

Tu verras que cette fonction passe par un maximum inférieur à 0.04812 (obtenu pour un angle de 1,05 radians environ)
Ainsi pour tous les triangles construits de cette manière:

Ou encore

Si on prend un périmètre p=4cm, on sait que l'aire A sera inférieure à 0.77 cm². Et la tienne valait 1cm²!

par **Noval** » 14 Juil 2007, 16:00

Merci beaucoup de tes réponses claires, je vais étudier ça!

EDIT: Pour le premier exo, je sais pas ce que sont les radians...

par **emdro** » 14 Juil 2007, 16:02

Le Québec se réveille? :dodo:

par **Noval** » 14 Juil 2007, 16:04

ouiahaha. Mais bon, j'ai pas encore étudié les radians donc ça pose peut-être problème?

par **emdro** » 14 Juil 2007, 16:07

Ca, c'est rien:
C'est juste une autre unité d'angles obtenue par proportionnalité:
180° correspond à

radians

Du coup, tu remplaces tous mes t radians par

,
et c'est parti!

par **Noval** » 14 Juil 2007, 16:14

d'accord, mais pourquoi RT vaudrait l'arc? J'aurais plutôt tendance à penser que ça vaudraut l'aire de la section...

Désolé de te prendre du temps, mais je ne comprends pas vraiment la proportionalité toujours le premier exo..

EDIT: Et que signifie dérive?

par **emdro** » 14 Juil 2007, 16:21

Dans un cercle, la longueur de l'arc est proportionnelle à l'angle au centre, de même que la surface du secteur circulaire. C'est intuitif, non?

Du coup:
pour la longueur:
0° donne 0
360° donne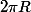

t° donne

la longueur de l'arc de cercle de rayon R et d'angle au centre t° est donc

. C'est d'ailleurs pour cela qu'on décide d'utiliser

qu'on nomme angle en radians.

pour l'aire:
0° donne 0
360° donne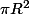

t° donne

Moi en radians, j'avais dit

, ce qui revient au même.

Ca va?

par **Noval** » 14 Juil 2007, 16:38

donc
Périmètre : t(pi)R/180 + 2R = 20
Aire: A= t(pi)R²/360

Si on isole R du périmètre:

360R + (pi)RT = 3600
R(360 + (pi)T) = 3600
R= 3600/(360+pi(t))

On remplace la valeur de R dans la formule de l'aire:

Ça nous donne t(pi)12960000 / 360(360t+(pi)t)²

?

Et là?

par **emdro** » 14 Juil 2007, 16:44

Noval a écrit:donc
Périmètre : t(pi)R/180 + 2R = 20
Aire: A= t(pi)R²/360

Si on isole R du périmètre:

360R + (pi)RT = 3600
R(360 + (pi)T) = 3600
R= 3600/(360+pi(t))

Oui

Pour la suite, non!

il y a un t en trop au dénomninateur. Et simplifie STP 3600²/360 !

Ensuite, tu étudies la fonction. Tu as déjà vu les dérivées?

par **Noval** » 14 Juil 2007, 16:46

"dirivée" ne me dis rien, cependant, en pratique, peut-être. Le vocabulaire de math varie ici et en france.

par **emdro** » 14 Juil 2007, 16:48

par **emdro** » 14 Juil 2007, 16:49

Si tu es très influencé par l'anglais (genre à 2km de l'Ontario!), tu dis peut-être différentielle! la dérivée de la fonction f se note f'. Ca c'est universel.

par **Noval** » 14 Juil 2007, 16:49

Oui j'y suis arrivé. ^^

par **Noval** » 14 Juil 2007, 16:50

Mais concrètement, c'est quoi?

par **emdro** » 14 Juil 2007, 16:52

C'est un outil (un peu compliqué, je ne peux pas t'expliquer ici: cela prend 2 mois de cours) pour savoir si une fonction est croissante ou décroissante, et donc trouver facilement son maximum.

comme tu ne connais pas, sors ta calculatrice, et demande-lui de tracer la courbe de la fonction obtenue. (t entre 0 et 180)

par **Noval** » 14 Juil 2007, 16:54

emdro a écrit:C'est un outil (un peu compliqué, je ne peux pas t'expliquer ici: cela prend 2 mois de cours) pour savoir si une fonction est croissante ou décroissante, et donc trouver facilement son maximum.

comme tu ne connais pas, sors ta calculatrice, et demande-lui de tracer la courbe de la fonction obtenue. (t entre 0 et 180)

Croissante, décroissante, maximum, c'est une parabole ça. On a fait ça tout l'année...

Cercles/Trigono

Qui est en ligne