Cercle inscrit dans un angle

[atreyyu]

Donné est un triangle . Cercle de centre est tangente au segment 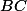et les lignes 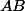et 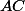aux points à l'extérieur du triangle. Montrer que la ligne 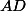passe par le centre du cercle circonscrit du triangle .

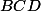Je crois que j'ai épuisé tout ce que je pourrait faire. S'il vous plaît aidez-moi.

[Ben314]

Salut,
Ton fameux cercle de centre D est un cercle "exinscrit" au triangle.
Son centre est le point de concours de 3 droites : la bissectrice intérieure issue de A et les bissectrices extérieures issues de B et de C (dans le triangle ABC).
La droite (AD ) est donc la bissectrice intériaure issue de A et, bien sûr, le centre du cercle inscrit est sur cette bissectrice.

Pour démontrer tout cela, il suffit de considérer les distances du point D à chacune des droites (AB), (AC) et (BC)...

[atreyyu]

Pour démontrer tout cela, il suffit de considérer les distances du point D à chacune des droites (AB), (AC) et (BC)...

Il me semble qu'ils sont tous égaux ... Mais qu'est-ce que je peux faire avec ça?

[oscar]

figure


ttp://yfrog.com/g4cercle12g

[oscar]

figureSoit D le centre du cercle demandé: D est équidistant des côtés de ABC


http://yfrog.com/0bcercle12g