Centre de Gravité et vecteurs

[youngfolks]

Bonjour, j'aurai besoin d'aide sur une question d'un de mes exercice sur mon DNS.

On considère les points A (-4;2), B (-1;4) et C(4;1) dans un repere carthésien (O, i, j)
1) calculer les coordonnées du points A' milieu de [Bc]
(j'ai trouvé : A' (1.5 ; 2.5). )

2) Calculer les coordonnées du point G, centre de gravité du triangle ABC

J'ai fait quelque recherche, pour cet exercice .. :
Soit G le centre de gravité du traingle ABC

AG = 2/3 AA'
Donc : AA'(5.5;4.5)
AG [2/3 (5.5; 4.5)]
AG (11/3; 3)
Mais ensuite, comment trouver les coordonnées de G...


Voici la figure :

[Arnaud-29-31]

Bonjour,

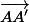
On a les coordonnées de A, celles de A' donc on peut déjà en déduire les coordonnées du vecteur . Ce que tu as fais ...

Puis comme tu as dis , , on trouve donc ...

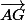
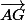
Tu as les coordonnées de A, celle de et on te demande celles de G ... Je ne vois pas ce qui bloque ...

[youngfolks]

Il faut soustraire les coordonnées de AG avec celle de A ?

[ned aero]

coordonnées de AG sont (xg -xa; yg-ya) avec xg -xa= 11/3 et yg-ya=3

et comme tu connais xa et ya....

ps: je n'ai pas vérifié tes calculs précédents