Un célèbre théorème à démontrer

[lapras]

le probleme initial : "démontrer pythagore" sans indication est difficile pour un éleve de seconde je pense ! Si on donne un indice avec le dessin on donne directement la réponse...

[Zweig]

Sinon,

Soit ABC un triangle rectangle en C avec AB = c, AC = b et BC = a. On trace la hauteur h issue de C sur (AB). On note H le point d'intersection et BH = p, PH = q.

On remarque que les triangles ABC, CBH et ACH sont semblables, d'où

i)

ii)

De i) on en tire et de ii), , d'où

[busard_des_roseaux]

bonsoir,


sinon, on pourrait partir de la conclusion (à démontrer)


et essayer de compléter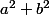 pour obtenir un carré parfait à gauche de l'égalité, d'où l'idée d'ajouter 2ab.

Cette idée se retrouve quand on essaye de factoriser
et que l'on ajoute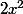

et ensuite le 2ab peut donner l'idée de "coller" deux triangles isométriques
sur les bords du carré de côté c.

mais évidemment,tout cela est capillotracté (tiré par les cheveux).

[Timothé Lefebvre]

Un exemple de solution (cellle que je privilégie pour le niveau seconde).

Pour démontrer que BC²=AB²+AC² on montre que la somme des angles du "petit" carré et du "moyen" carré vaut l'aire du "grand".

Sur mon schéma j'ai tracé le carré ABDE de côté AB (le petit),
le carré ACFG de côté AC (le moyen),
et le carré BCHI (le grand) de côté BC.
De plus, j'ai tracé AW la hauteur issue de A et coupant BC perpendiculairement en W, et donc HI perpendiculairement en X.

On doit donc montrer que Aire(BCHI) = Aire(ABDE) + Aire(ACFG)

Procédure :

• Démontrer que Aire(ABDE) = 2 Aire(DBC)

• Démontrer que Aire(ACFG) = 2 Aire(BCF)

• Démontrer que DBC et ABI sont isométriques et en déduire que : Aire(ABDE)= 2 Aire(ACH)

• Démontrer que BCF et ACH sont isométriques et en déduire que : Aire(ACFG) = 2 Aire(ACH)

• Démontrer que Aire(BWXI) = 2 Aire(ABI) et Aire(WCHX) = 2 Aire(ACH)

De là on en déduit que : Aire(BCHI) = Aire(ABDE) + Aire(ACFG) et donc le théorème de Pythagore.