Calul d'une primitive

[novicemaths]

Bonjour

Je vais calculer une primitive de

Je pense à une forme de avec et

On réécrit la fonction

J'en déduit que

Est-ce que mon calcul est correct ?

A bientôt

[Ben314]

Salut,
Tu n'a qu'à vérifier en dérivant . . .
Aprés, de mon temps (mais c'est vrai que ça date pas mal), la dérivée de c'était donc en particulier, celle de , c'était plutôt mais peut être que dans un soucis de simplicité, on a enlevé le 2 depuis que j'ai pris ma retraite.
Et d'un autre coté, je comprend absolument pas la façon dont tu rédige : ton , il ne désigne pas un réel ? Et si oui, tu peut m'expliquer ce que ça veut dire ?
(moi je sais dériver des fonctions, mais dériver un réel, de mon temps, ça n'avait pas de sens . . .)

[novicemaths]

Bonsoir

Est-ce que j'aurais dû présenter le calcul ainsi

A bientôt

[Ben314]

Est-ce que j'aurais dû présenter le calcul ainsi

Non, c'est aussi totalement incohérent.
Oublie le contexte et regarde uniquement cette égalité que contient ta prose :
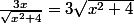
Tu en pense quoi ?
Bien sûr, vu le contexte, on se doute que ce que tu as voulu dire, c'est qu'une primitive du terme de gauche, c'est le terme de droite, sauf que de dire qu'une primitive de f c'est F, ben ça ne s'écrit surement pas f=F (*)

Et, personnellement, ce que j'aurais écrit, c'est que :
Si alors
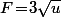
Donc une primitive de est , c'est à dire la fonction définie par

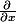
Bien noter que les "primes", ben il se placent sur les fonctions et pas sur les réels : ce qui a du sens, c'est et pas . Si tu veut utiliser ce type de truc (dériver une "formule" et pas une fonction), il y a une notation "à la physicienne" qui est , mais qui n'est que très moyennement appréciée à un niveau élémentaire de mathématiques (mais ça devient utile ensuite lorsque l'on aborde les fonctions de plusieurs variables)

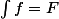
(*) Bien que personnellement je n'aime pas du tout cette notation, je sais que certains écrivent pour traduire le fait que F est une des primitive de f.