Calculs de primitives.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 14:38
par Blup » 04 Aoû 2010, 14:38
Bonjour, j'aurai aimé savoir comment faire pour calculer les primitives suivantes :

et

Sans avoir recours à une intégration par parties.
Pour la première, on peut trouver la primitive avec la formule donnant u^n ce qui me paraît étrange c'est que cette formule ne peut être utilisé seulement dans le cas où u=x et non dans le cas où u représente une fonction usuelle quelconque.
Merci d'avance.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Aoû 2010, 14:40
par Nightmare » 04 Aoû 2010, 14:40
Salut,
la première est de la forme

avec u(x)=x+2 et n=1/2
la deuxième est de la forme

-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 14:47
par Blup » 04 Aoû 2010, 14:47
Merci pour ta réponse Nightmare, mais je ne connais pas la deuxième formule que tu m'as donné. Pourrais-tu la donner entièrement s'il te plaît ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Aoû 2010, 15:20
par Nightmare » 04 Aoû 2010, 15:20
Quelle est la dérivée de

lorsque u est une fonction dérivable?
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 15:28
par Blup » 04 Aoû 2010, 15:28
Nightmare a écrit:Quelle est la dérivée de

lorsque u est une fonction dérivable?

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Aoû 2010, 15:30
par Nightmare » 04 Aoû 2010, 15:30
Non ! Regarde tes formules.
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 15:33
par Blup » 04 Aoû 2010, 15:33
Ah, on utilise la formule d'une fonction composée. Soit

*
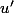
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 15:52
par Blup » 04 Aoû 2010, 15:52
Donc, ça donne

.
Merci.
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 18:26
par Blup » 04 Aoû 2010, 18:26
Re, la primitive de
})
?
Je sais que cela donne
 ))
mais je ne vois pas comment.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Aoû 2010, 18:36
par girdav » 04 Aoû 2010, 18:36
Blup a écrit:Re, la primitive de
})
?
Je sais que cela donne
 ))
mais je ne vois pas comment.
On a le logarithme à une certaine puissance fois sa dérivée.
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 18:42
par Blup » 04 Aoû 2010, 18:42
Cela donne d'après ce que tu m'as écrit :

Ln(x)^(-1)
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 04 Aoû 2010, 18:43
par Euler07 » 04 Aoû 2010, 18:43
En fait

avec
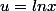
(quand x>0)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Aoû 2010, 18:44
par girdav » 04 Aoû 2010, 18:44
On a un truc de la forme
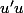
donc une primitive de tout ça est
|+C)
.
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 18:51
par Blup » 04 Aoû 2010, 18:51
Euler 07 a écrit:En fait

avec
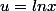
(quand x>0)
Oui, sauf que si tu transformes l'expression comme ça, tu risques d'appliquer la formule : u'*u^n qui dans ce cas là, n'aboutit à pas grand chose.
Merci de votre aide.
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 04 Aoû 2010, 18:59
par Euler07 » 04 Aoû 2010, 18:59
Blup a écrit:Oui, sauf que si tu transformes l'expression comme ça, tu risques d'appliquer la formule : u'*u^n qui dans ce cas là, n'aboutit à pas grand chose.
Merci de votre aide.
Tu veux dire plutôt que la dérivée de

Mais je ne parlais pas de la formule u'*u^n
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 04 Aoû 2010, 19:05
par Blup » 04 Aoû 2010, 19:05
Non, je faisais bien référence à la formule u'*u^n avec n = -1 dans ce cas là.
La primitive de sin(5x) donne (-cos(5x)/5) pourquoi ?
Sachant que la seule formule qu'on a à notre disposition est : primitive de sin (x) donne -cos(x) +c.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Aoû 2010, 10:23
par Nightmare » 11 Aoû 2010, 10:23
Salut,
il ne faut pas oublier que primitiver est l'inverse de dériver ! Ainsi, on retrouve des formules très simple, comme par exemple que si F est une primitive de f, alors une primitive de f(ax) est F(ax)/a (pour t'en rendre compte, dérive F(ax)/a voir ce qu'on trouve)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 105 invités
