Calculs d'intégrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 11 Sep 2010, 14:18
par eratos » 11 Sep 2010, 14:18
Salut.
On me demande de calculer l'intégrale de

Pour me guider un peu, on dit dans le bouquin qu'on reconnait la dérivée d'une fonction composée.
Donc je pose u(t)= 3t et je suis bloqué. comment je fais? quelle propriété j'utilise ici? :briques:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Sep 2010, 14:38
par Sa Majesté » 11 Sep 2010, 14:38
Salut
Quelle est la dérivée de sin(3t) ?

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 11 Sep 2010, 15:13
par eratos » 11 Sep 2010, 15:13
J'ai trouvé =)
u(t)= 3t
u'(t)=3
En utilisant la relation comme quoi l'intégrale de pi/6 à pi/3 de u'cosu est

(comment dit-on ça proprement?)
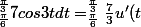cos(ut)dt= [{\frac{7}{3}sin 3t]\bigint_{\frac{\pi}{6}}^{\frac{\pi}{3}}=F(b)-F(a))
Après ça coule de source:
-F(a)= \frac{7}{3} (sin 3\frac{\pi}{3} - sin3\frac{\pi}{6}) = \frac{7}{3} (0-1)= -7/3)

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Sep 2010, 15:18
par Sa Majesté » 11 Sep 2010, 15:18
OK ça m'a l'air bon :++:

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 13 Sep 2010, 19:43
par eratos » 13 Sep 2010, 19:43
Re!
J'ai un nouveau souci avec une primitive cette fois.
Donc voilà la fonction à "primitiver" (=p):
= \frac{1}{4x-1}+\frac{3}{(4x-1)^2})
définie sur ]1/4;

[
Voilà ce que j'ai fait:
J'ai posé X= 4x-1 pour me faciliter la tâche, comme je suis fainéant.
= \frac{1}{X}+\frac{3}{X^2})
, ainsi:
F(x)=

C'est ici que le drame arrive, je regarde dans mon bouquin le corrigé, et j'ai presque juste sauf qu' on me dit:
= \frac{1}{4x-1}+\frac{3}{(4x-1)^2})
=
= \frac{1}{4}.\frac{4}{4x-1}+\frac{3}{4}\frac{4}{4(4x-1)^2}) Pourquoi?
Pourquoi?après cela:
=\frac{1}{4}ln(4x-1)-\frac{3}{4}.\frac{1}{(4x-1)})
=\frac{1}{4}ln(4x-1)-\frac{3}{4(4x-1)})

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 13 Sep 2010, 19:56
par Sa Majesté » 13 Sep 2010, 19:56
eratos a écrit:J'ai un nouveau souci avec une primitive cette fois.
Donc voilà la fonction à "primitiver" (=p):
= \frac{1}{4x-1}+\frac{3}{(4x-1)^2})
définie sur ]1/4;

[
Voilà ce que j'ai fait:
J'ai posé X= 4x-1 pour me faciliter la tâche, comme je suis fainéant.
Tu crois que ça facilite mais c'est en réalité piégeant
eratos a écrit:= \frac{1}{X}+\frac{3}{X^2})
, ainsi:
F(x)=

Tu voulais dire
= \ln X- \frac{3}{X})
je suppose ?
En posant X=4x-1=h(x) tu fais un changement de variable
 = \frac{1}{x}+\frac{3}{x^2})
) = \frac{1}{4x-1}+\frac{3}{(4x-1)^2} = f(x))
Tu as trouvé une primitive G de g
 = \ln x - \frac{3}{x})
et tu l'appliques à h(x)=4x-1 et tu penses avoir trouvé une primitive de f
Mais ça ne marche pas car quand tu dérives G(h(x)) tu obtiens
)' = G'(h(x)) \times h'(x) = g(h(x)) \times h'(x) = 4 f(x))
car h'(x)=4
Ce 4 est mis en facteur dans la solution car c'est la dérivée de 4x-1

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 18 Sep 2010, 20:20
par eratos » 18 Sep 2010, 20:20
Je comprend pas très bien. Je dois mettre les fractions au même numérateur?
J'ai un nouveau souci mais c'est pour demain, là je suis mort et pas envie de me prendre la tête avec les balises TEX. :marteau:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 113 invités
[
, ainsi: