Calculer une dérivée terminale (pour la 3eme fois)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cpwjuz
- Membre Naturel
- Messages: 33
- Enregistré le: 28 Oct 2020, 00:16
-
 par cpwjuz » 28 Oct 2020, 22:12
par cpwjuz » 28 Oct 2020, 22:12
Bonsoir,
j'ai la fonction
=12xe^{0.0018x^2-0.195x})
,
je calcule sa dérivée :
e^{0.0018x^2-0.195x})
e^{0.0018x^2-0.195x})
e^{0.0018x^2-0.195x})
Or la dérivée correcte a un
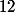
après le
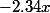
.
Comment trouver le
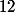
?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 28 Oct 2020, 22:37
par Pisigma » 28 Oct 2020, 22:37
Bonsoir,
ta dérivée après "je calcule sa dérivée" est déjà fausse
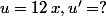
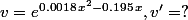
-
cpwjuz
- Membre Naturel
- Messages: 33
- Enregistré le: 28 Oct 2020, 00:16
-
 par cpwjuz » 28 Oct 2020, 23:20
par cpwjuz » 28 Oct 2020, 23:20
ahhh Pisigma, j'ai du mal avec les dérivées


Donc:
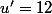
et
e^{0.0018x^2-0.195x})
et donc :
-0.195)e^{0.0018x^2-0.195x})
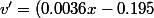e^{0.0018x^2-0.195x})
Ensuite :
e^{0.0018x^2-0.195x})
Mais à partir de là, je ne vois pas comment faire puisque je suis censé trouver
e^{0.0018x^2-0.195x})
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 28 Oct 2020, 23:33
par Pisigma » 28 Oct 2020, 23:33
à partir de "Ensuite" c'est faux
'=u'v+u\,v')
-
mathou13
- Membre Relatif
- Messages: 204
- Enregistré le: 08 Juin 2019, 14:52
-
 par mathou13 » 28 Oct 2020, 23:57
par mathou13 » 28 Oct 2020, 23:57
Bonjour,
u(x)=12x v(x)=e^(0.0018x^2-0.195x)
u'(x)=12 v'(x)=(0.0036x-0.195)e^(0.0018x^2-0.195x)
f(x)=u(x)v(x)
f'(x)=u'(x)v(x)+u(x)v'(x)=.....
-
cpwjuz
- Membre Naturel
- Messages: 33
- Enregistré le: 28 Oct 2020, 00:16
-
 par cpwjuz » 29 Oct 2020, 00:02
par cpwjuz » 29 Oct 2020, 00:02
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 29 Oct 2020, 06:58
par Pisigma » 29 Oct 2020, 06:58
de rien

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 181 invités

