Calculer une aire

[cyprento]

Bonjour, j'ai un petit problème

Voici l'énoncé de mon exercice : http://prntscr.com/6stq5f
Voici ce que j'ai fais : http://prntscr.com/6stqfn

et je ne sais pas comment faire, arrivé à ce stade là pour calculer l'aire, merci !

[WillyCagnes]

bjr

tu as trouvé la bonne formule de l'aire Lxl, en général on prend x comme inconnue mais cela marche aussi avec l

A(l)=125l-2l²

l'aire est maxi pour A'(l)=0

calcules donc la dérivée de l'aire=?
tu devrais trouver l=125/4

et l'aire maxi= (125-2l)xl

[Whoever]

Salut,

Ce qui tu as fait est bien. Il ne te reste plus qu'à trouver l'aire maximale.

On met ce que t'as trouvé sous forme d'une fonction qui exprime l'aire en fonction de la largeur :



Tu remarques que c'est une fonction polynôme du second degré avec : a = -2 ; b = 125 ; c = 0
Tu as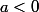 donc, le maximum de la fonction est atteint en .

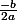Ce qui te donne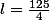 . L'aire est maximale quand la largeur vaut .

Au final, tu as donc une aire maximale de

[cyprento]

Merci de ta réponse mais je t'avoues que j'ai du mal à comprendre

Aussi que veux tu dire quand tu me demandes de calculer la dérivée de l'aire, et comment m'y prendre ?

[WillyCagnes]

désolé, si tu n'as pas vu le calcul des dérivées, alors utilise la méthode de Whoever

[cyprento]

Merci beaucoup à vous deux, je pense avoir terminer, corrigez moi si erreur
http://prntscr.com/6su2dl

[Whoever]

Tu as oublié ces parenthèses : Aire = l x L = l x (125 - 2l)

Ensuite, il est préférable de présenter ta fonction sous la forme ax² + bx + c pour bien qu'on se rende compte que c'est un polynôme du second degré. N'hésite pas à le préciser, d'ailleurs. Car si ce n'était pas une fonction polynôme du second degrés, tu ne pourrais pas utiliser -b / 2a.

Tu n'as pas finit l'exercice car l'énoncé te demande l'aire maximale est non la largeur pour laquelle l'aire est maximale. Donc complète avec A(125/4).

[cyprento]

Je pense avoir finis
http://prntscr.com/6suenb

[Whoever]

Oui c'est tout bon ! :lol3:

[Ben314]

Salut,
Perso, pour un problème de ce genre, j'attendrais qu'on me dise entre quelles bornes peut varier la... variable de la fonction, c'est à dire l.