Calculer la somme S= 3+33+333+...+33...3 (dernier terme n ch

[spaldy]

Bonjour,
Je dois faire cet exercice:
Calculer la somme S= 3+33+333+...+33...3 (dernier terme composé de n chiffres)
Mais je ne vois absolument pas comment faire, (je suis complètement perdu en maths). Si vous avez des solutions à me proposer merci d'avance

[siger]

Bonsoir

333333 ....33 = 3*( 1111...111) = 3 *( 10^0+10^1+10^2 + ....10^n)
somme geometrique de raison 10
d'ou sauf erreur
= 3*(10^(n-1) -1)/9 = 10^(n-1)/3 - 1/3


puis on trouve encore une somme geometrique en additionnant tout les nombres 3,33,333.......

[nodjim]

Pour moi, c'est 3*(1234567890123456789012....) n étant le nb de chiffres du nombre entre parenthèses.

[nodjim]

Ce n'est pas tout à fait ça. En fait, c'est 370370370....
Si on veut connaitre le final selon n, c'est un peu plus compliqué, mais c'est faisable.

[zygomatique]

salut

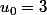
S est la somme des termes de la suites définies par et

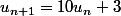
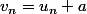
1/ déterminer le réel a tel que la suite définie par soit géométrique

2/ exprimer v_n puis u_n en fonction de n

3/ calculer S

:zen:

[spaldy]

Ok merci :++: je n'y serais jamais arrivé seul.

[chan79]

Si on met des 1 à la place des 3

1
11
111
1111
11111 ici n=5

chaque ligne s'écrit pour i variant de 0 à n-1

soit

Il faut donc calculer







on multiplie par 3 pour obtenir la somme demandée:

[nodjim]

Ben oui mais si on devait l'écrire en chiffres ?

[chan79]

Ben oui mais si on devait l'écrire en chiffres ?

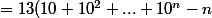On écrit n fois le 1; on met un 0 à droite, on enlève n et on divise par 3

Exemple avec n=8

111111110-8= 111111102

111111102:3=37037034