Bonjour, j'ai un dm a faire pendant les vacances sur le produit scalaire et je m'en sors vraiment pas...
ABCD est un carré de côté x ; I et J sont les milieux respectifs de [BC] et [CD]. On note a une mesure en degré de l'angle IAJ.
En calculant de deux façons le produit scalaire AI.AJ , déterminer une valeur approchée de a à 0.1 degrés près.
Merci d'avance.
Calculer un produit scalaire
9 messages
- Page 1 sur 1
Salut !
Par définition :
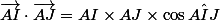) .
.
Déduis-en alors) en fonction de
en fonction de  ,
, 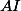 ,
,  .
.
Exprime alors en fonction de ,
, 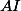 et
et  puis le vecteur
puis le vecteur  sachant que
sachant que 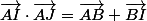\cdot \(\vec{AD}+\vec{DJ}\)) .
.
Par définition :
Déduis-en alors
Exprime alors en fonction de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
louloutte_du_94 a écrit:Bonjour, j'ai un dm a faire pendant les vacances sur le produit scalaire et je m'en sors vraiment pas...
ABCD est un carré de côté x ; I et J sont les milieux respectifs de [BC] et [CD]. On note a une mesure en degré de l'angle IAJ.
En calculant de deux façons le produit scalaire AI.AJ , déterminer une valeur approchée de a à 0.1 degrés près.
Merci d'avance.
bonjour
en supposans le carre dans le sens direct
en developpant les vecteurs
cos(AI;AJ)=2/3
(AI;QJ)=arccos(2/3)=19,412 degres
louloutte_du_94 a écrit:Oui je suis arrivée jusqu'ici en fait ! Et j'ai trouvé que AI= x+(x/2) et AJ= x+(x/2) et après je bloque pour le produit scalaire..
bonjour,
attention AI^2= AB^2+BI^2 ....
dans le cas du calcul d'un produit scalaire la " technique" est de decomposer les vecteurs en utilisant le theorems de Chasles pour faire apparaitre:
des produits de vecteurs perpendiculaires, donc nuls
des produits de vecteurs colinéaires, donc egaux au produit des normes
(AI.AJ) = (AB + BI).(AD + DJ)
avec AB.AD =0, BJ.DJ = 0
BI.AD = BI*AD = x* x/2
......
louloutte_du_94 a écrit:Euh bah moi j'ai juste appliqué la formule ! Norme du vecteur AB = racine carre de((xB-xA) + (yB-yA))
Tu veux dire :
Norme du vecteur AB = racine carre de((xB-xA)^2 + (yB-yA)^2)
Comme le dit siger, il s'agit ici du Théorème de Pythagore dans les triangles ABI et ADJ rectangles respectivement en B et D!
Donc AI^2 = AB^2 + BI^2 ...
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
