bonjour j aurais besoin d aide pour un exercice pas tres dur mais je n arrive pas a l argumenter
1)l entier 7056 est il un carre???
2)l entier 2007²-2005² est il un entier premier??
3)l entier 2007au cube-2005 au cube est il un entier premier???
il precis que cela doit etre fait sans calculatrice et il attent des arguments
merci d avance si vous pouvais m aider
Calcule de carre
13 messages
- Page 1 sur 1
tytony313 a écrit:bonjour j aurais besoin d aide pour un exercice pas tres dur mais je n arrive pas a l argumenter
1)l entier 7056 est il un carre???
2)l entier 2007²-2005² est il un entier premier??
3)l entier 2007au cube-2005 au cube est il un entier premier???
il precis que cela doit etre fait sans calculatrice et il attent des arguments
merci d avance si vous pouvais m aider
1)l entier 7056 est il un carre??? Que réponds-tu (même sans arguments) ? Et quels sont tes arguments, ou à quoi penses-tu comme arguments possibles ?
1)l entier 7056 est il un carre???
Tous les réels positifs sont des carrés ! En particulier 7056 est le carré de et également de
et également de  . Tu n'as donc nul besoin d'une calculatrice pour répondre !
. Tu n'as donc nul besoin d'une calculatrice pour répondre !
S'il s'agissait de savoir si 7056 est un "carré parfait", expression réservée aux nombres rationnels carrés de rationnels, ou aux entiers carrés d'entiers, alors il faudrait décomposer 7056 en produit de facteurs premiers et ainsi trouver sa racine carrée. Mais la question n'est pas celle-là !
2)l entier 2007²-2005² est il un entier premier
Il est évident qu'il s'agit d'un entier, puisque différence de deux carrés d'entiers, ces derniers étant entiers ! Donc la question se résume à
"s'agit-il d'un nombre premier ou pas ?"
Et si tu essayais de factoriser l'expression 2007²-2005² ?
Tous les réels positifs sont des carrés ! En particulier 7056 est le carré de
S'il s'agissait de savoir si 7056 est un "carré parfait", expression réservée aux nombres rationnels carrés de rationnels, ou aux entiers carrés d'entiers, alors il faudrait décomposer 7056 en produit de facteurs premiers et ainsi trouver sa racine carrée. Mais la question n'est pas celle-là !
2)l entier 2007²-2005² est il un entier premier
Il est évident qu'il s'agit d'un entier, puisque différence de deux carrés d'entiers, ces derniers étant entiers ! Donc la question se résume à
"s'agit-il d'un nombre premier ou pas ?"
Et si tu essayais de factoriser l'expression 2007²-2005² ?
Bonjour
Une autre piste pour les questions 2) et 3) :
2005 et 2007 sont des entiers naturels impairs
Le carré (le cube) d'un entier naturel impair est un .... ....
La différence de deux ... ... est un entier naturel pair.
Un entier naturel pair est multiple de 2.
Aucun entier naturel multiple de 2 (sauf 2 lui-même) n'est premier.
Comme il est évident que ni 2007²-2005² ni 2007³-2005³ ne vaut 2, ...
Qu'as-tu trouvé pour (a-b) ?j ai commencer comme sa mais pour savoir sil sont premier ou pas???
Une autre piste pour les questions 2) et 3) :
2005 et 2007 sont des entiers naturels impairs
Le carré (le cube) d'un entier naturel impair est un .... ....
La différence de deux ... ... est un entier naturel pair.
Un entier naturel pair est multiple de 2.
Aucun entier naturel multiple de 2 (sauf 2 lui-même) n'est premier.
Comme il est évident que ni 2007²-2005² ni 2007³-2005³ ne vaut 2, ...
Ce n'est pourtant pas difficile !
Il est évident que 2007²-2005² est un entier ! Mais est-ce un entier premier ?
a²-b²=(a+b)*(a-b)
Donc 2007²-2005² = (2007+2005)*(2007-2005) = 4012*2
Il est donc clair que 2007²-2005², produit de 4012 par 2 n'est pas premier !
De même, en vertu de l'identité remarquable :
citée ci-dessus, identité que tu ne connais peut-être pas, mais que tu devrais apprendre (elle est très utile !),
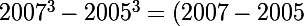\times (2007^2+2007*2005+2005^2))
...il est clair que est le produit de 2 par un grand nombre ! Par conséquent c'est un nombre pair qui n'est donc pas premier !
est le produit de 2 par un grand nombre ! Par conséquent c'est un nombre pair qui n'est donc pas premier !
Sans aller jusque là, c'est-à-dire sans utiliser cette identité remarquable, tu peut simplement constater que le carré (resp. le cube) d'un nombre impair est forcément impair, et que tout comme
tout comme  est la différence entre deux nombres impairs et que par conséquent c'est un nombre pair, donc non premier puisqu'il est différent de 2, le seul premier pair !
est la différence entre deux nombres impairs et que par conséquent c'est un nombre pair, donc non premier puisqu'il est différent de 2, le seul premier pair !
Il est évident que 2007²-2005² est un entier ! Mais est-ce un entier premier ?
a²-b²=(a+b)*(a-b)
Donc 2007²-2005² = (2007+2005)*(2007-2005) = 4012*2
Il est donc clair que 2007²-2005², produit de 4012 par 2 n'est pas premier !
De même, en vertu de l'identité remarquable :
Quidam a écrit:
citée ci-dessus, identité que tu ne connais peut-être pas, mais que tu devrais apprendre (elle est très utile !),
...il est clair que
Sans aller jusque là, c'est-à-dire sans utiliser cette identité remarquable, tu peut simplement constater que le carré (resp. le cube) d'un nombre impair est forcément impair, et que
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
