Calcul D'une Somme...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 09 Juil 2006, 13:37
par krokos55 » 09 Juil 2006, 13:37
Bonjour je viens de finir une term S , j'aimerais bien votre aide afin de calculer:
Sigma des k.k! pour k allant de 1 à n
merci beaucoup
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 09 Juil 2006, 13:51
par krokos55 » 09 Juil 2006, 13:51
oui tout a fait ! c'est ce que je voudrais calculer...
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 09 Juil 2006, 14:11
par aviateurpilot » 09 Juil 2006, 14:11
c'est un exo olympiad?
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 09 Juil 2006, 14:30
par krokos55 » 09 Juil 2006, 14:30
c'est un exo que je dois faire pour la futur rentrée... :--: :hum: :mur:
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 09 Juil 2006, 14:55
par Mikou » 09 Juil 2006, 14:55
C'est quoi lenoncé exact ( questions qui precedent, eventuellement )
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 09 Juil 2006, 15:03
par Sdec25 » 09 Juil 2006, 15:03
Salut
j'ai trouvé une solution en m'inspirant des sommes géométriques (S-qS) :
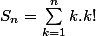
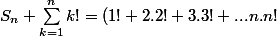 + (1! + 2! + ... + n !) \; = \; 1!(1+1) + 2!(2+1) + ... + n!(n+1) = \sum_{k=1}^n (k+1)!)
Donc
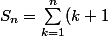! - \sum_{k=1}^n k! = \sum_{k=2}^{n+1} k! - \sum_{k=1}^n k! = (n+1)! - 1)
La somme est donc égale à (n+1)! - 1
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 09 Juil 2006, 16:48
par krokos55 » 09 Juil 2006, 16:48
merci beaucoup ...c'est très gentil !
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 10 Juil 2006, 01:14
par krokos55 » 10 Juil 2006, 01:14
puisque vous m'avez si bien aidé pour le calcul précédent , je suis dans la meme galere pour ce calcul ci
calculons Sigma des q^k pour k allant de 1 à n
MErci beaucoup par avance
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 10 Juil 2006, 01:28
par Sdec25 » 10 Juil 2006, 01:28
pas de problème :happy2:
Tu n'as pas vu les sommes géométriques en terminale ?
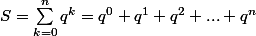
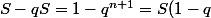)
Donc
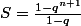
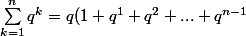 = q \frac{1-q^n}{1-q})
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 10 Juil 2006, 11:28
par krokos55 » 10 Juil 2006, 11:28
si je l'ai vu mais il y a quelque chose que je ne comprend pas c'est pourquoi on utilise S-qS pour calculer S...
c'est la seule méthode ? une astuce ?
merci
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 10 Juil 2006, 12:11
par Sdec25 » 10 Juil 2006, 12:11
C'est une astuce qui permet de ne laisser que 2 termes : le premier et le dernier.
C'est quand même plus pratique d'avoir une somme de 2 termes qu'une somme de n termes.
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 10 Juil 2006, 18:29
par krokos55 » 10 Juil 2006, 18:29
ok je vois mais a quoi correspond le q dans S-qS ?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 10 Juil 2006, 18:55
par Sdec25 » 10 Juil 2006, 18:55
q est la raison de la suite géométrique.
S = 1 + q + q^2 + ... + q^n
q x S = q + q^2 + ... + q^{n+1}
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 10 Juil 2006, 19:32
par krokos55 » 10 Juil 2006, 19:32
oui mais parfois on a pas affaire à une suite géométrique ...
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 10 Juil 2006, 19:33
par krokos55 » 10 Juil 2006, 19:33
Pour calculer la premiere somme de la discussion par exemple ?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 10 Juil 2006, 19:38
par Sdec25 » 10 Juil 2006, 19:38
Il faut faire au cas par cas.
Pour la première somme j'ai vu qu'en rajoutant k à chaque terme on obtenait la somme de k!
Il n'y a pas de règle, il faut essayer tout ce qu'on peut.
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 15 Juil 2006, 04:10
par Nicolas_75 » 15 Juil 2006, 04:10
Bonjour,
Tout cela me semble bien compliqué.
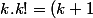!-k!)
et on est donc face à une somme téléscopique. Le résultat est immédiat.
Nicolas
-
krokos55
- Membre Naturel
- Messages: 84
- Enregistré le: 30 Avr 2006, 11:32
-
 par krokos55 » 25 Juil 2006, 10:15
par krokos55 » 25 Juil 2006, 10:15
somme téléscopique ? résultats immédiats? je ne comprend pas...pourrais tu m'éxpliquer ? merci beaucoup
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Juil 2006, 12:17
par Nicolas_75 » 25 Juil 2006, 12:17
On remarque que
!-k! = (k+1)\cdot k!-k!= k.k!)
Donc
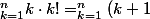!-k! = (n+1)! - 1! = (n+1)! - 1)
Deux lignes.

Nicolas
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
