Calcul d'une somme de carrés
43 messages
- Page 2 sur 3 - 1, 2, 3
Le peu que j'en connait, Algobox, ça a justement été inventé pour "éviter de faire peur aux élèves" (je suis pas sûr qu'on s'en serve bien en dehors des Lycées)
Après, et ce que c'est réellement efficace, c'est à dire et est-ce que effectivement "ça fait moins peur aux élèves", ça j'en sais rien...
Après, et ce que c'est réellement efficace, c'est à dire et est-ce que effectivement "ça fait moins peur aux élèves", ça j'en sais rien...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour moi, au niveau lycée, c'est le pseudo basic de la calculatrice qui devrait servir; Algobox n'a pas un langage génial; par exemple ,il faut écrire N prend la valeur 0 au lieu de 0->N; si on utilise sinon, il demande la condition donc la fonction Else n'existe pas en fait; impossible de faire appel à un sous programme et des particularités du genre si A==B ou si A!=B ou x²=pow(x,2); sans compter qu'il ne donne que 8 chiffres significatifs!
Son seul intérêt est sa rapidité et on peut sans problème simuler 500000 fois une expérience aléatoire; en fait, il ne sert qu'à ça (pour moi).
Son seul intérêt est sa rapidité et on peut sans problème simuler 500000 fois une expérience aléatoire; en fait, il ne sert qu'à ça (pour moi).
paquito a écrit:Je te montre un programme, mais si tu ne te renseignes pas très vite, ce modèle n'auras servi à rien!
1 VARIABLES
2 k EST_DU_TYPE NOMBRE
3 Sn EST_DU_TYPE NOMBRE
4 n EST_DU_TYPE NOMBRE
5 DEBUT_ALGORITHME
6 Sn PREND_LA_VALEUR 0
7 LIRE n
8 POUR k ALLANT_DE 1 A n
9 DEBUT_POUR
10 Sn PREND_LA_VALEUR Sn+k*k
11 FIN_POUR
12 AFFICHER "Sn="
13 AFFICHER Sn
14 FIN_ALGORITHME
ça n'a pas l'air trop compliqué! la boucle c'est pour k allant de 1 à n, ça veut dire que quand la boucle commence on ajoute 1² à 0² (Sn est initialisée à 0), puis k prend la valeur 2 et on ajoute 2² à 1² et ça continue jusqu'à ce que l'on ait ajouté tous les carrés de 1² à n² pour avoir Sn. tu peux essayer de faire le même mais avec Sn=0+1+2+3+..+k+.....+n.
Merci grâce a toi j'ai compris. En faite je n'avais jamais utilisé de boucle auparavant donc c'est pour ça que je n'arrivais pas a programmer.
bonjour ...vues les réponses ci-dessus...j'approuve.
Toutefois , préciser votre type de calculatrice (Casio 35+ / TI82/83) pour avoir ce programme ...qui sera , peut-être pas très bien disposé ,car je ne maîtrise pas encore la communication en clair bien que le latex m'est maintenant familier...Confirmant ce qui dit ci-dessus vous avez intérêt à connaitre le vocable anglosaxon (instructions plus courtes et plus concises...sauf si vous avez une TI 82 stat.fr).
La programmation , c'est passionnant ,mais pensez à vos autres devoirs !
Toutefois , préciser votre type de calculatrice (Casio 35+ / TI82/83) pour avoir ce programme ...qui sera , peut-être pas très bien disposé ,car je ne maîtrise pas encore la communication en clair bien que le latex m'est maintenant familier...Confirmant ce qui dit ci-dessus vous avez intérêt à connaitre le vocable anglosaxon (instructions plus courtes et plus concises...sauf si vous avez une TI 82 stat.fr).
La programmation , c'est passionnant ,mais pensez à vos autres devoirs !
sxmwoody a écrit:bonjour ...vues les réponses ci-dessus...j'approuve.
Toutefois , préciser votre type de calculatrice (Casio 35+ / TI82/83) pour avoir ce programme ...qui sera , peut-être pas très bien disposé ,car je ne maîtrise pas encore la communication en clair bien que le latex m'est maintenant familier...Confirmant ce qui dit ci-dessus vous avez intérêt à connaitre le vocable anglosaxon (instructions plus courtes et plus concises...sauf si vous avez une TI 82 stat.fr).
La programmation , c'est passionnant ,mais pensez à vos autres devoirs !
J'ai déjà fait mon algorithme sur Algobox et je n'ai pas besoin de le programmer sur une calculatrice.
Toutefois, Merci de votre aide
Re-Salut !
La relation R (ou égalité), te dit que pour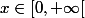 ,
, -\sigma(x)=(x+1)^2) donc :
donc :
- Quelle égalité a-t-on en remplaçant x par 0 ?
- Quelle égalité a-t-on en remplaçant x par 1 ?
- Quelle égalité a-t-on en remplaçant x par 2 ?
...
- Quelle égalité a-t-on en remplaçant x par n ?
Tu obtiens ainsi (sans toutes les énumérer), n+1 égalités. Somme les membres à membres et tu auras le résultat voulu :+++:
Clemo a écrit:C'est bon j'ai réussi la question 4 !!!
Maintenant il faudrait m'aider pour la question 5 que je remet si dessous
5. Soit n un entier naturel. Ecrire la relation R pour x=0, 1, 2,...., n, puis en déduire l'expression de S(n) en fonction de n. Calculer S(100)
La relation R (ou égalité), te dit que pour
- Quelle égalité a-t-on en remplaçant x par 0 ?
- Quelle égalité a-t-on en remplaçant x par 1 ?
- Quelle égalité a-t-on en remplaçant x par 2 ?
...
- Quelle égalité a-t-on en remplaçant x par n ?
Tu obtiens ainsi (sans toutes les énumérer), n+1 égalités. Somme les membres à membres et tu auras le résultat voulu :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Re-Salut !
La relation R (ou égalité), te dit que pour,
donc :
- Quelle égalité a-t-on en remplaçant x par 0 ?
- Quelle égalité a-t-on en remplaçant x par 1 ?
- Quelle égalité a-t-on en remplaçant x par 2 ?
...
- Quelle égalité a-t-on en remplaçant x par n ?
Tu obtiens ainsi (sans toutes les énumérer), n+1 égalités. Somme les membres à membres et tu auras le résultat voulu :+++:
On obtient toujours 1.
Que veut tu dire par " Somme les membres à membres et tu auras le résultat voulu"?
Clemo a écrit:On obtient toujours 1.
Que veut tu dire par " Somme les membres à membres et tu auras le résultat voulu"?
Non, on n'obtient pas toujours
Par exemple, pour
Si tu as deux égalités a=b et c=d, alors en sommant membre à membre (côté gauche avec côté gauche et côté droit avec côté droit), tu as
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Clemo a écrit:Mais nan 2-1=1 et pas 2²
Oui, mais tu as enlevé les "
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Clemo a écrit:Ca change quoi?
Ca change quoi ? Ben ça change que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
43 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
