Calcul d'une distance (nombres complexes)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Déc 2009, 22:58
par Dinozzo13 » 18 Déc 2009, 22:58
Bonsoir, ce soir je bute sur le calcul d'une distance, pourriez-vous m'aider, merci d'avance.
On défini les points
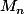
d'affixe
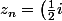^n(1+i\sqrt3))
où

.
On me demande de calculer la distance
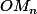
, mais je bloque :
Je calcule :
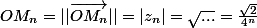
, mais ce n'est pas ça, j'en suis sûr.
-
zaze_le_gaz
- Membre Relatif
- Messages: 293
- Enregistré le: 27 Nov 2009, 21:31
-
 par zaze_le_gaz » 18 Déc 2009, 23:02
par zaze_le_gaz » 18 Déc 2009, 23:02
comment tu as fait pour calculer ton module?
rappel:/z1*z2/=/z1/*/Z2/ avec / / ma notation pour module

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Déc 2009, 23:12
par Ben314 » 18 Déc 2009, 23:12
Un truc qui m'étonne un peu, c'est que, dans z_n,... il y a pas de n (ou alors c'est mes lunettes qui sont sales :zen: )
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Déc 2009, 23:13
par Dinozzo13 » 18 Déc 2009, 23:13
éh bien je trouve
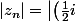^n(1+i\sqrt 3)\right|=\left|\left(\frac{1}{2}i\right)^n\right|\left|1+i\sqrt 3\right|=4\left|\frac{1}{2}i\right|^n=\frac{1}{4^{n-1}})
-
zaze_le_gaz
- Membre Relatif
- Messages: 293
- Enregistré le: 27 Nov 2009, 21:31
-
 par zaze_le_gaz » 18 Déc 2009, 23:13
par zaze_le_gaz » 18 Déc 2009, 23:13
d'où vient cette puissance n?
edit: merveilleux tour de magie, je la vois maintenant

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Déc 2009, 23:14
par Ben314 » 18 Déc 2009, 23:14
C'est tout bon, sauf les deux dernières égalités...
Rappel : ne pas confondre le module et... le carré du module !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Déc 2009, 23:14
par Dinozzo13 » 18 Déc 2009, 23:14
Ben314 a écrit:Un truc qui m'étonne un peu, c'est que, dans z_n,... il y a pas de n (ou alors c'est mes lunettes qui sont sales :zen: )
:ptdr: on a rien vu ^^
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Déc 2009, 23:17
par Dinozzo13 » 18 Déc 2009, 23:17
Dinozzo13 a écrit:éh bien je trouve
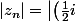^n(1+i\sqrt 3)\right|=\left|\left(\frac{1}{2}i\right)^n\right|\left|1+i\sqrt 3\right|=4\left|\frac{1}{2}i\right|^n=\frac{1}{4^{n-1}})
Bon alors on a
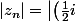^n(1+i\sqrt 3)\right|=\left|\left(\frac{1}{2}i\right)^n\right|\left|1+i\sqrt 3\right|=2\left|\frac{1}{2}i\right|^n=\frac{1}{2^{n-1}})
Là ça à l'air bon ^^

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Déc 2009, 23:20
par Ben314 » 18 Déc 2009, 23:20
Impec.......
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Déc 2009, 23:22
par Dinozzo13 » 18 Déc 2009, 23:22
wii trop bien merci, ça va me permettre de pouvoir finir l'exo ^^
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Déc 2009, 23:34
par Dinozzo13 » 18 Déc 2009, 23:34
A la fin, on me demande d'exprimer en fonction de n :
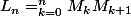
je trouve :
}{2^{n}})
Puis enfin la limite : vaut
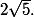
Etes-vous d'accord avec tout ça ?
-
zaze_le_gaz
- Membre Relatif
- Messages: 293
- Enregistré le: 27 Nov 2009, 21:31
-
 par zaze_le_gaz » 18 Déc 2009, 23:46
par zaze_le_gaz » 18 Déc 2009, 23:46
oui ca parait bon

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Déc 2009, 23:47
par Ben314 » 18 Déc 2009, 23:47
En ce qui me concerne, ça roule....
Tu as fait un dessin pour "voir" ce que tu as calculé ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Déc 2009, 00:24
par Dinozzo13 » 19 Déc 2009, 00:24
oui, c'était demandé lors de la 1re question de l'exo et ça concorde ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités