Calcul
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
KingTiti24
- Membre Relatif
- Messages: 160
- Enregistré le: 30 Oct 2008, 15:33
-
 par KingTiti24 » 19 Fév 2009, 21:48
par KingTiti24 » 19 Fév 2009, 21:48
Bonjour à tous , voici un calcul ou je suis bloqué:
(x au carré + 16) + (x+4)(x+5) - 8x+ (4-x)(x+10)>ou égal 0
Comment factorier cela de manière à pouvoir faire mon tableau de signe... :help:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Fév 2009, 21:52
par Timothé Lefebvre » 19 Fév 2009, 21:52
Salut,
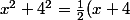^2 + \frac{1}{2}(x-4)^2)
(identité remarquable)
A toi la suite.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 19 Fév 2009, 21:52
par uztop » 19 Fév 2009, 21:52
Bonjour,
si on écrit l'expression de la façon suivante, la factorisation devient beaucoup plus simple à voir :
x²-16 + (x+4)(x+5) - 8x+ 32 + (4-x)(x+10)
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 19 Fév 2009, 21:53
par uztop » 19 Fév 2009, 21:53
Timothé Lefebvre a écrit:Salut,
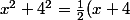+\frac{1}{2}(x-4))
(identité remarquable)
A toi la suite.
ben qu'est ce que tu nous fait Timothé ? Ca ne marche pas ton truc
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Fév 2009, 21:54
par Timothé Lefebvre » 19 Fév 2009, 21:54
Ah ?
Tu es sûr ? Mon identité est fasse ?
EDIT : merde j'ai zappé les carrés ! Je corrige !
-
ChaoX
- Messages: 6
- Enregistré le: 19 Fév 2009, 21:33
-
 par ChaoX » 19 Fév 2009, 21:56
par ChaoX » 19 Fév 2009, 21:56
euh....
Je pense pas qu'il travaille dans les complexes:
x²+4²=1/2(x+4)(x-4)
ca donne quelque chose de bizarre:
x²=-48
possible mais je ne comprend pas le rapport avec son inéquation :help:
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 19 Fév 2009, 21:57
par uztop » 19 Fév 2009, 21:57
@Tim oui c'est juste mais je n'ai pas l'impression que ça simplifie les calculs.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Fév 2009, 21:58
par Timothé Lefebvre » 19 Fév 2009, 21:58
J'avais oublié les carrés

J'ai corrigé.
Si il bosse dans les complexes on a alors :
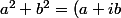(a-ib))
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 19 Fév 2009, 21:59
par uztop » 19 Fév 2009, 21:59
On va finir par l'embrouiller, ce que j'ai écrit
x²-16 + (x+4)(x+5) - 8x+ 32 + (4-x)(x+10)
permet de factoriser avec des identité remarquables de niveau seconde, je pense que c'est ce qui est attendu ici
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Fév 2009, 21:59
par Timothé Lefebvre » 19 Fév 2009, 21:59
uztop a écrit:@Tim oui c'est juste mais je n'ai pas l'impression que ça simplifie les calculs.
Je sais que je passe pour un malade à chaque fois avec ces identités inutiles mais au moins ça nous file un autre facteur facil en plus des deux !
-
KingTiti24
- Membre Relatif
- Messages: 160
- Enregistré le: 30 Oct 2008, 15:33
-
 par KingTiti24 » 19 Fév 2009, 22:00
par KingTiti24 » 19 Fév 2009, 22:00
Oui ca je sais pas bien mais surtout pour trouver un facteurs commun quoi... en plus je sent que le -8x doit servir à quelque chose :doh:
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 19 Fév 2009, 22:03
par uztop » 19 Fév 2009, 22:03
au fait, est ce que tu es sur de ta formule de départ, ça ne serait pas
(x² + 16) + (x-4)(x+5) - 8x+ (4-x)(x+10)
?
Ca serait beaucoup plus simple.
-
ChaoX
- Messages: 6
- Enregistré le: 19 Fév 2009, 21:33
-
 par ChaoX » 19 Fév 2009, 22:03
par ChaoX » 19 Fév 2009, 22:03
Pour l'inéquation:
(x+10)(4-x) si tu met un signe - tu peux inverser une des deux parentheses...
x²-16==> identité remarquable
(x+4)(x+5)==> déjà factorisée.
-8x+32==> factorisation par -8
Voila tout ce qui peut t'aider sans donner la solution maintenant a toi de jouer :zen:
j'ai un probleme avec l'inequation de base: elle change tout le temps dans chaque post....
Donc si les parties que je te donne sont bonnes dit le sinon je réadapte la factorisation.
-
KingTiti24
- Membre Relatif
- Messages: 160
- Enregistré le: 30 Oct 2008, 15:33
-
 par KingTiti24 » 19 Fév 2009, 22:05
par KingTiti24 » 19 Fév 2009, 22:05
uztop a écrit:au fait, est ce que tu es sur de ta formule de départ, ça ne serait pas
?
Ca serait beaucoup plus simple.
Non non c'est x+4 sur et justement cela surprend beaucoup de monde :briques:
-
KingTiti24
- Membre Relatif
- Messages: 160
- Enregistré le: 30 Oct 2008, 15:33
-
 par KingTiti24 » 19 Fév 2009, 22:05
par KingTiti24 » 19 Fév 2009, 22:05
ChaoX a écrit:Pour l'inéquation:
(x+10)(4-x) si tu met un signe - tu peux inverser une des deux parentheses...
x²-16==> identité remarquable
(x+4)(x+5)==> déjà factorisée.
-8x+32==> factorisation par -8
Voila tout ce qui peut t'aider sans donner la solution maintenant a toi de jouer :zen:
Oui mais c'est x carré + 16 :triste:
-
ChaoX
- Messages: 6
- Enregistré le: 19 Fév 2009, 21:33
-
 par ChaoX » 19 Fév 2009, 22:09
par ChaoX » 19 Fév 2009, 22:09
en fait si je comprend:
dans les termes "libres" non factorisés tu as:
x²
+16
-8x
+32
bon partant de la ca fait:
x²-8x+48=(x-4)²-16+48=(x-4)²+32
donc partant de la en seconde et premiere tu es coincé :++:
et en terminale tu galere :king2:
RAHHHHHHHHHHHHHHH
Qui m'a sorti le 32?!?!?!?!
x²-8x+16=(x-4)²-16+16 factorisation avec la forme canonique vu en seconde.
Sot au final (x-4)²
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 19 Fév 2009, 22:12
par uztop » 19 Fév 2009, 22:12
oui effectivement, si l'expression donnée est juste, je ne vois pas comment la factoriser en seconde (au fait, tu es bien en seconde ?)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Fév 2009, 22:13
par Timothé Lefebvre » 19 Fév 2009, 22:13
Forme canonique en seconde ?
Euh non, en première oui !
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 19 Fév 2009, 22:13
par uztop » 19 Fév 2009, 22:13
ChaoX a écrit:Sot au final (x-4)²
oui, mais il y a un terme en x+4 au milieu qui gène
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Fév 2009, 22:14
par Timothé Lefebvre » 19 Fév 2009, 22:14
Après une rapde recherche ([url="http://www.maths-forum.com/showthread.php?t=82716"]http://www.maths-forum.com/showthread.php?t=82716[/url]) il est donc bien certain que ce jeune homme est en seconde (ou du moins était en seconde le 15 fevrier) donc oublions celà !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
