Le x représente un réel (voire un complexe) quelconque. On applique ensuite la formule en prenant pour x les valeurs 0,1,2,...,n.
Si tu veut trouver le résultat avec des intégrales, l'idée consiste à chercher une fonction f (en fait un polynôme) tel que, pour tout

dans

, on ait
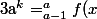\,dx\ \ (1))
.
Cela permettra d'écrire que :
\,dx+\bigint_{1}^2 f(x)\,dx+\bigint_{2}^3 f(x)\,dx+...+\bigint_{n-1}^n f(x)\,dx\ =\ \bigint_{0}^n f(x)\,dx)
qui se calcule facilement.
Pour trouver f, on peut écrire que c'est un polynôme (de degrés k) de coefficients inconnus et on cherche les valeurs que doivent avoir les coeffs. pour que la formule
)
soit vérifiée.
P.S. Par rapport à ton post précédent, il faut effectivement noter que la formule
)
peut s'écrire
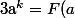-F(a-1))
où

est une des primitives de

.
On peut donc parfaitement chercher

plutôt que

...
