Calcul racine ènième (Terminale S)

[Nicolas2012]

Bonjour, je pensais savoir mais en fait non :marteau:

Voici mon problème, je vais essayer d'utiliser le mode "belles formules" mais je ne vous promets rien, essayons, sachant que 5 racine carré troisième, je l'écris: 3sqrt{5} pour indication.

(sqrt{15^4} * 4sqrt{3} * 3sqrt{5}) / sqrt{3^7} * 4sqrt(5}) = ?

Selon le correcteur, la réponse serait 3^(-5/4) * 5^(1*3) hors moi je trouve: 3^(59/28) * 5^(25/12) et j'ai refait plusieurs fois le calcul, je ne vois pas où je me trompe. Ma version:

= (3^2 * 5^2 * 3^(1/4) * 5^(1/3)) / (3^(1/7) * 5^(1/4))
= (3^(9/4) / 3^(1/7)) / (5^(7/3) / 5^(1/4))
= (3^(9/4) * 5^(7/3)) / 3^(1/7) * 5^(1/4))
= 3^(9/4 - 1/7) * 5^(7/3 - 1/4)
= 3^(59/28) * 5^(25/12)

Où mon raisonnement devient-il faux, à quel niveau? Merci d'avance!

Nicolas2012

[Nicolas2012]

C'est ce que je craignais, la formule n'a pas pris en compte le "n-ième" devant "sqrt"... désolé pour le format, pas top... :--:

[ampholyte]

Bonjour,

D'après ce que tu as marqué, je comprends ça :



Est-ce cela ou est-ce plutôt :



Utilise ce tuto pour écrire correctement les formules : http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php

Sinon met un screen de l'énoncé.

[Nicolas2012]

Bonjour ampholyte, OK, grâce à ta réponse (son code) je vais essayer de répondre avec le mode TEX, car à ta question, la réponse est 1, sauf que tu t'es trompé sur le dernier membre, j'essaye.
J'ai essayé hier mais impossible de trouver la formule "racine n-ième" dans ton tuto, je l'avais lu pourtant :lol3:



Voilà, et l'auteur trouve en réponse:

, soit:

Et moi, je ne trouve pas ça, j'écris mon raisonnement, si possible en format TEX:



=

=

=

Bon, ce sera pas parfait mais d'après ce que je vois en prévisualisation, c'est quand même bien plus lisible. A vos corrections! :id:

[ampholyte]

Bon personnellement le résultat est très curieux :

Je décompose :







On a donc :



Je trouve la même chose ici :
http://www.mathway.com/answer.aspx?p=prec?p=(SMB20(15SMB074)SMB15*SMB154SMB20(3)SMB15*SMB153SMB20(5))SMB10(SMB20(3SMB077)*SMB20(5SMB074))?p=7?p=?p=?p=?p=?p=0?p=?p=0?p=?p=?p=Simplify

PS :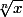 est la racine n-ieme de x à ne pas confondre avec qui est la racine carrée de

[Nicolas2012]

Re,

Oui, tu as raison, après une nouvelle étude du pb, j'ai vu que je m'étais bien planté sur , c'est pas du tout égal à , tu as raison, j'ai confondu les racines n_ième et les normales :bad:

En revanche, je vais regarder ta correction ce soir pour voir qui a raison, mais je te crois car même en me plantant, je trouvais leur réponse bizarre. Merci ampholyte! :we:

[ampholyte]

Pas de quoi, je suppose qu'il y a soit une erreur dans l'énoncé ou dans la correction. Ce sont des choses qui arrivent malheureusement.

Si tu veux le faire chez toi, essaye d'abord de simplifier le plus possible. J'ai essayé d'écrire une ou deux étapes mais en barrant les doublons et en décomposant 15 en 3*5 le résultat vient très rapidement.

[Nicolas2012]

Si tu veux le faire chez toi, essaye d'abord de simplifier le plus possible. J'ai essayé d'écrire une ou deux étapes mais en barrant les doublons et en décomposant 15 en 3*5 le résultat vient très rapidement.[/quote]

Hello,

Effectivement, merci pour les conseils, super!
Bonne soirée à toi, au plaisir. :lol3:

[Nicolas2012]

Bonjour ampholyte,

J'aurais dû lire ta réponse en détail avant car ta réponse est bonne mais je crois que je me suis mal exprimé (à cause du TEX), quand dans la formule j'ai écrit "4 racine quatrième de 3" (je ne sais pas si on dit comme ça), tu as écris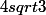 , hors, oui, ta réponse est exacte, le seul hic c'est que ma question n'est pas 4racine de 3 mais bien 4 racine quatrième de 3 donc "racine carré de 3 avec "en haut à gauche le 4"

C'est sur ça que j'ai du mal, pas sur le calcul avec 4racine de 3, mais c'est ce que je te disais au début, je ne sais pas comment faire les racines n-ièmes sur TEX.

Donc la formule en littéraire, c'est: numérateur: "racine carré de 15^4 * racine quatrième de 3 * racine troisième de 5" / par le dénominateur: "racine carré de 3^7 * racine carré de 5^4"

Et j'ai vérifié à la calculatrice, pour le moment, mes calculs sont bons, le truc, c'est que je ne sais pas comment simplifier au-delà.

Dernière équation que je trouve, c'est:

= numérateur: * ( * 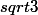) / 3 (le dénominateur)

Et là, je n'arrive plus à simplifier, de l'aide? Merci.


P.S: j'ai essayé de remettre 5^(1/3) en racine n-ième mais comme on a racine carré de 5 et racine carré de 3... pas de simplication, je suis pas plus avancé... :mur: