Calcul de probabilité insersection et union

[novicemaths]

Bonsoir

Soit une probabilité P est un univers et deux évènement A et B tel que:



Calculer

Je sais que la formule normalement est

si je ne fais pas erreur devient

Et là, je ne vois pas comment faire le calcule ?

A bientôt

[Mateo_13]

Bonjour,

si je ne fais pas erreur devient

Pourquoi ?

Fais un dessin, dessine un grand ensemble Omega, puis à l'intérieur un ensemble A et un autre B qui l'intersecte, puis colorie et observe que ce n'est pas .

En revanche, la même formule que tu as citée auparavant devrait fonctionner en remplaçant B par

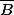
Cordialement,
--
Mateo.

[novicemaths]

Bonsoir

Si j'ai bien compris

A bientôt

[lyceen95]

Tu sais que
Bien. Tu en sais assez pour faire plein de choses, c'est la formule qu'il faut savoir.
Cette formule, on peut aussi l'écrire :

Les 2 lettres et représentent des ensembles, n'importe quels ensembles de notre univers
Et donc, en particulier, peut être l'ensemble
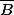
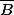
Et en remplaçant par , ça donne :