Calcul probabilité conditionnelle

[novicemaths]

Bonjour

J'ai un petit soucis avec un petit exercice de probabilité conditionnelle.

On a P(A)=0,09 et P(B) = 0,65 et

Je souhaite résoudre .

J'ai essayé de le résoudre ci-dessous.



Pourriez-vous me donner les règles de calculs de ce genre d'exercice ?

A bientôt

[lyceen95]

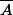
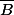
Je ferais un tableau, avec 3 lignes ( , et total ), 3 colonnes (, et total), et je remplirais ce tableau à partir des chiffres donnés au début.
Puis je lirais le résultat sur ce tableau.

[catamat]

Bonjour
Ceci dit le calcul que tu donnes est complètement faux, le reprendre suivant les conseils de lycéen95.
La seule formule à utiliser ici est p("A union B")=p(A)+p(B)-p("A inter B")

[novicemaths]

Bonjour

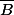
C'est le qui me perturbe un peut.

Est-ce que le calcul ci-dessous est correct ?



A bientôt

[catamat]

Non, je me répète c'est mieux si tu suis la méthode préconisée par Lycéen95

Mais tu tiens à utiliser des formules, on peut utiliser celle là :



et aussi