Voici la suite en question :
Je vois qu'il y a une forme indéterminée qu'il faut lever pour calculer la limite, mais je ne vois pas comment commencer. Quelqu'un pourrait-il me guider dans la bonne direction ?
Je vous remercie d'avance.
Calcul de la limite d'une suite
2 messages
- Page 1 sur 1
Calcul de la limite d'une suite
par lentis » 05 Nov 2023, 14:13
Bonjour,
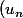Voici la suite en question :_{n\ge 0}=\sqrt{n}(\frac{e^{\sqrt{n+1}}}{e^{\sqrt{n-1}}}-1))
Je vois qu'il y a une forme indéterminée qu'il faut lever pour calculer la limite, mais je ne vois pas comment commencer. Quelqu'un pourrait-il me guider dans la bonne direction ?
Je vous remercie d'avance.
Voici la suite en question :
Je vois qu'il y a une forme indéterminée qu'il faut lever pour calculer la limite, mais je ne vois pas comment commencer. Quelqu'un pourrait-il me guider dans la bonne direction ?
Je vous remercie d'avance.
Re: Calcul de la limite d'une suite
par Ben314 » 05 Nov 2023, 16:04
Salut,
(1)
.
(2)}=\dfrac{b_n}{\sqrt{n}})
où la suite_{n\geq 1})
tend vers 
donc _{n\geq 1})
tend vers 0.
(3)=\dfrac{b_n}{a_n}\big(e^{a_n}\!-\!1\big)=b_n\!\times\!\dfrac{e^{a_n}\!-\!e^0}{a_n-0})
tend vers 1 vu que tend vers 1 et que 
tend, lorsque 
tend vers 0, vers \!=\!\exp(0)\!=\!1)
(1)
(2)
où la suite
(3)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :