Bonsoir à tous!
Svp m'aider à résoudre cette limite:
lim x *ln((x+1)/(x-1)) lorsque x tend vers plus l'infini
A l'aide de la calculatrice je la trouve 2 mais je n'arrive pas à la démontrer.
J'attends vos réponses!!!
Calcul limite de fonction log nép
4 messages
- Page 1 sur 1
Re: Calcul limite de fonction log nép
Je dirais la chose suivante, si tu as vu les développements limités :
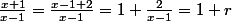 avec
avec 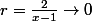 quand
quand 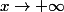
Donc = xln(1+r)) . Puisque
. Puisque 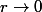 quand
quand 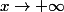 on peut appliquer un développement limité de
on peut appliquer un développement limité de ) : on a
: on a  = r + o(r)) quand
quand 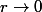 ,
, ) représentant quelque chose de négligeable devant
représentant quelque chose de négligeable devant  (autrement dit ln(1+r) est grossièrement équivalent à
(autrement dit ln(1+r) est grossièrement équivalent à  c'est à dire ici
c'est à dire ici 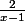 )
)
Conclusion : \rightarrow x \times \frac{2}{x-1} \rightarrow 2) quand
quand 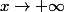
J'essaye de voir si on peut faire ça sans passer par les DL avec les outils de terminale
Donc
Conclusion :
J'essaye de voir si on peut faire ça sans passer par les DL avec les outils de terminale
Re: Calcul limite de fonction log nép
Bonjour,
Une autre solution , assez classique si on a les développements limités,
artificielle sinon :
pour x>1 , on pose t=1/x , ainsi x=1/t , et t<1 .
t tend vers 0 pour x tendant vers +infini
le calcul donne
f(x)=(1/t).(ln(1+t) - ln(1-t)) et les développements limités classiques (ordre 1)
permettent de conclure
sans développement limité (Terminale)
f(x)=(ln(1+t))/t - (ln(1-t))/t
et on conclue par la définition de la dérivée en 0, pour les fonctions u et v
u(t)=ln(1+t) et v(t)=ln(1-t)
assez artificiel.
De toute façon un changement de variable ne me semble pas être un objectif de Terminale.
qu'en pensez vous ?
Une autre solution , assez classique si on a les développements limités,
artificielle sinon :
pour x>1 , on pose t=1/x , ainsi x=1/t , et t<1 .
t tend vers 0 pour x tendant vers +infini
le calcul donne
f(x)=(1/t).(ln(1+t) - ln(1-t)) et les développements limités classiques (ordre 1)
permettent de conclure
sans développement limité (Terminale)
f(x)=(ln(1+t))/t - (ln(1-t))/t
et on conclue par la définition de la dérivée en 0, pour les fonctions u et v
u(t)=ln(1+t) et v(t)=ln(1-t)
assez artificiel.
De toute façon un changement de variable ne me semble pas être un objectif de Terminale.
qu'en pensez vous ?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
