Calcul intégral
32 messages
- Page 1 sur 2 - 1, 2
Calcul intégral
Bonjour!
Voici l'énoncé, je n'y arrive pas du tout et c'est pour demain. Le problème c'est qu'en faisant les graphiques, les fonctions ne se croisent pas.. Du coup je n'ai pas de surface à calculer..
" Représentez (et hachurez-là) la surface délimitée par les courbes (dont on donne les équations) et calculez la valeur (précise!) de l'aire de cette surface.
y = ln(x+2) ; y = x/2 +1 ; x = -1 ; x = 2 "
Merci beaucoup si vous savez m'aider, c'est pour demain :mur:
Voici l'énoncé, je n'y arrive pas du tout et c'est pour demain. Le problème c'est qu'en faisant les graphiques, les fonctions ne se croisent pas.. Du coup je n'ai pas de surface à calculer..
" Représentez (et hachurez-là) la surface délimitée par les courbes (dont on donne les équations) et calculez la valeur (précise!) de l'aire de cette surface.
y = ln(x+2) ; y = x/2 +1 ; x = -1 ; x = 2 "
Merci beaucoup si vous savez m'aider, c'est pour demain :mur:
bonjour,
comme les deux courbes ne se croisent pas,
le domaine à quarrer (quarrer =calculer sa mesure d'aire en carreaux)
est située , verticalement, entre les deux courbes et
horizontalement entre les droites verticales
d'équation x=-1 et x=2
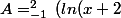 - (0.5 x +1) \right) dx) en unité d'aire u.a
en unité d'aire u.a
la fonction affine se primitive à vue et le log par parties
comme les deux courbes ne se croisent pas,
le domaine à quarrer (quarrer =calculer sa mesure d'aire en carreaux)
est située , verticalement, entre les deux courbes et
horizontalement entre les droites verticales
d'équation x=-1 et x=2
la fonction affine se primitive à vue et le log par parties
mathelot a écrit:bonjour,
comme les deux courbes ne se croisent pas,
le domaine à quarrer (quarrer =calculer sa mesure d'aire)
est située , verticalement, entre les deux courbes et
horiontalement entre les droites verticales
d'équation x=-1 et x=2en unité d'aire u.a
la fonction affine se primitive à vue et le log par parties
D'accord merci! Pour la primitive en partie je suis bloquée là :
f(x) = ln(x) -> f'(x) = 1/x
g'(x) = x+3 -> g(x) = x²/2 +3x
donc ln. (x²/2) + 3x -
Et pour l'autre j'ai :
0.25x^4 + x
mathelot a écrit:zut, je me suis trompé, je corrige, la courbe du log est sous la droite et pas au dessus
de la droite.
Aire
Je ne comprends pas du tout.
Je suis toujours bloquée à:
[ (x+2)ln(x+2)-x-(1/4)x^2-x] avec 2 au dessus de ']' et -1 en dessous.
Logiquement je dois juste remplacer x par 2 et soustraire avec x remplacé par -1 non?
EDIT : Ah.. Du coup je dois remplacer quoi ou?
Kidrauhpe a écrit:Je ne comprends pas du tout.
Je suis toujours bloquée à:
[ (x+2)ln(x+2)-x-(1/4)x^2-x] avec 2 au dessus de ']' et -1 en dessous.
Logiquement je dois juste remplacer x par 2 et soustraire avec x remplacé par -1 non?
EDIT : Ah.. Du coup je dois remplacer quoi ou?
on doit intégrer de 2 à -1.
est ce que tu vois pourquoi on a l'opposé et non pas le bon résultat ?
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
